摘  要： 在實時的交通路況中,，路徑規(guī)劃的核心問題是快速而有效地找到從起點到達終點的最優(yōu)路線。將PSO算法應用到的路徑規(guī)劃中來,，針對實時變化的交通路況,，在適應度函數(shù)中引入懲罰項來實現(xiàn)靜態(tài)和動態(tài)下的路徑規(guī)劃，并通過引入變異算子的操作來避免該算法陷入局部最優(yōu),。實驗表明,，改進后的PSO算法搜索效率高，時間開銷隨路網(wǎng)規(guī)模的擴大增幅較小,，適用于大規(guī)模路網(wǎng)和動態(tài)路徑規(guī)劃,。

　　關鍵詞： 車載導航；路徑規(guī)劃,；變異算子,；局部最優(yōu)

0 引言

　　路徑規(guī)劃是車載導航系統(tǒng)的基本功能，由于其有較強的應用價值,，國內外學者對此進行了深入的研究[1-3]?，F(xiàn)今較流行的算法有Dijstra算法（簡稱D算法）和A*算法，但D算法搜索速度較慢,，A*算法搜索速度快但成功率不高,，且這些算法只能在靜態(tài)地圖上進行路徑規(guī)劃，沒有考慮實時變化的交通狀況,。近年來,，智能算法因其強大的搜索能力而被廣泛應用于路徑規(guī)劃中。楊易[4]把遺傳算法與A*算法相結合,，提高路徑規(guī)劃算法的效率,；王健[5]把蟻群算法應用到導航的路徑規(guī)劃中,，但其沒有考慮隨時間的動態(tài)變化因素；于海璁等人[6]提出了一種適用于多模式路徑規(guī)劃的遺傳算法,，可用于個性化的路徑導航,。本文將PSO算法應用到車載導航的路徑規(guī)劃中，引入變異算子解決PSO算法的局部最優(yōu)問題,，不僅擁有較快的收斂速度,，還能增強全局搜索能力。

1 粒子群算法的描述

　　粒子群算法由Eberhart博士和Kennedy博士在1995年提出[7],，它通過粒子間的協(xié)作和信息共享來尋找最優(yōu)解,。算法在搜索時，根據(jù)粒子自身歷史的最佳位置pbest和種群內所有粒子歷史的最佳位置gbest的基礎上進行位置變化,，其速度和位置公式如下：

　　其中,，t表示迭代次數(shù)，r1,、r2是（0,，1）之間的隨機數(shù)，c1,、c2為學習因子,，w為慣性權重，其表達式為：

　　其中wmax,、wmin為權重的最大和最小值，tmax為最大迭代次數(shù),。

2 粒子群算法在路徑規(guī)劃中的應用

　　本章節(jié)的主要內容是解決粒子的編碼和適應度函數(shù)的構造,，編碼方式涉及粒子位置和速度的更新操作，適應度函數(shù)用來評價粒子的適應值,。最后還解決了PSO算法自身陷入局部最優(yōu)的問題,。

　　2.1 粒子編碼

　　編碼即粒子位置的表達方式，是設計粒子群優(yōu)化和應用操作的關鍵問題,，根據(jù)路徑規(guī)劃的實際情況,，本文采用直觀、方便的實數(shù)編碼[8],。粒子狀態(tài)表達方式如式（4）所示,，編碼方式如式（5）所示。

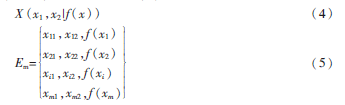
　　其中,，f（x）表示適應值,，m表示粒子個數(shù)。

　　2.2 適應度函數(shù)

　　2.2.1 適應度函數(shù)的設計

　　將粒子群算法用于路徑規(guī)劃時,，適應度函數(shù)的設計使得該算法不僅能夠在靜態(tài)網(wǎng)絡下獲得最優(yōu)路徑,，通過增加懲罰項M[9]也能適用于實時變化的交通狀況,，其適應度函數(shù)定義為：

　　（1）當0<n<0.5時,，暢通,；

　　（2）當0.5≤n<0.75時,，微擁擠狀態(tài),；

　　（3）當0.75≤n≤1時,，嚴重擁堵狀態(tài),。

　　針對不同的擁堵狀態(tài)采用不同的適應度函數(shù)。

　　適應度函數(shù)主要取決于是否有交通擁堵等狀況,，車載導航儀[10]將接收到的交通信息轉換成路段的相關特性數(shù)據(jù),，同時給出交通擁堵系數(shù)n，并根據(jù)n的大小選擇相應的適應度函數(shù),。采用該適應度函數(shù)的優(yōu)點是占用的存儲空間少,，并根據(jù)實時的交通狀況找出最佳路徑。

　　2.2.2 適應度函數(shù)對路徑規(guī)劃的影響

　　如圖1所示,，粒子群的起點為S,，終點為D。粒子群從S點開始搜索,，若不定義適應度函數(shù),，則粒子隨機選擇移動方向，而根據(jù)適應度函數(shù)（式（6））,，大部分粒子選擇更靠近終點的右方,，小部分粒子選擇左方，如圖1（a）所示,。當粒子到達下一路口時,，重新計算自身適應值，并共享當前全局最優(yōu)解,，各個粒子根據(jù)式（1）,、（2）更新自身的速度與方向。因此,，在單位時間段內,，沿著上方行走的粒子數(shù)量高于其他方向的粒子數(shù)，同時這些粒子記錄自身的局部最優(yōu)解,，也能得到全局最優(yōu)解,。后續(xù)粒子選擇路徑時會受這些最優(yōu)解的影響，沿著粒子較多的方向前進,，也有小部分粒子會選擇其他方向來尋求更短的路徑,，如圖1（b）所示,。當某個粒子到達終點時，其他粒子將會收到該粒子共享的信息,，所有粒子將會朝該方向前進,，如圖1（c）所示。

　　2.3 解決陷入“局部最優(yōu)”的問題

　　為了避免PSO陷入“局部最優(yōu)”,，本文在PSO算法中引入變異算子,，其思想是：當算法達到特定的迭代次數(shù)h之后，除去之前擁有全局最優(yōu)解的粒子外,，計算其他粒子與當前全局最優(yōu)值gbest的距離,，若距離小于閾值，則取這些粒子的百分比重新初始化,，使這部分粒子重新尋找最優(yōu)值,，使種群獲得更高的粒子多樣性，擴大搜索范圍,，避免粒子群算法陷入局部最優(yōu),，同時能夠增強全局搜索能力。帶變異算子的粒子群算法如下：

　　If（t<tmax&&>h）

　　取滿足dp-gbest<DistValue粒子中的百分比,，并根據(jù)式（1）,、（2）對其速度與位置進行重新初始化；

　　Else

　　按式（1）,、（2）更新粒子速度和位置,；

　　End

　　其中，t為當前迭代次數(shù),，tmax為最大迭代次數(shù),，h為特定的迭代次數(shù)，dp-gbest表示粒子的當前點到全局最優(yōu)解gbest的距離,，DistValue為設定的距離值。

3 算法驗證與分析

　　為了驗證上述算法的可行性,，本文根據(jù)上海市松江區(qū)部分實際地圖抽象得到的路網(wǎng)數(shù)據(jù)結構進行實驗,，如圖2所示。

　　其中路段數(shù)為134,，路口數(shù)為92,，粒子數(shù)為95，最大迭代次數(shù)為200,，wmax=0.9,，wmin=0.4，c1=c2=2,。最優(yōu)路徑標準采用最短路徑,，PSO算法的路徑規(guī)劃結果如圖3所示,，D算法路徑規(guī)劃的結果如圖4所示。

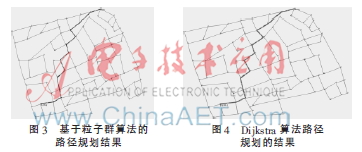
　　由圖3和圖4可知,，D算法規(guī)劃出的最優(yōu)路徑與粒子群算法的最優(yōu)路徑是一樣的,，但兩個算法的搜索時間不同，D算法搜索時間為46 ms,，粒子群算法搜索時間為55 ms,。

　　上述結果是在實際地圖上進行的小規(guī)模節(jié)點數(shù)的實驗，圖5和圖6是對大規(guī)模節(jié)點數(shù)進行仿真的結果比較,。

　　由圖5可知,，PSO算法和D算法在節(jié)點數(shù)相當?shù)那闆r下，算法求得的路徑長度是相同或相似的,，但由圖6可知,，由于D算法與PSO算法的原理和收斂方式不同，在節(jié)點數(shù)目較少時,，PSO算法需要更多的時間,，但是隨著節(jié)點數(shù)目的增加，PSO算法的收斂速度較D算法明顯要快,，在大規(guī)模路網(wǎng)中,，PSO算法具有較大優(yōu)勢。

　　最后當在路段中設置嚴重交通擁堵,，即0.75≤n≤1時,，其路徑規(guī)劃的結果如圖7所示。

　　由圖7可知,，當在道路上設置擁堵路段時,，算法重新規(guī)劃出了一條避開擁堵路段的最優(yōu)路徑，相比于只能夠運用在靜態(tài)路網(wǎng)的D算法,，該算法更具有實際意義,。

4 結論

　　本文將粒子群算法用于路徑規(guī)劃中，從粒子的編碼規(guī)則到適應度函數(shù)的設計,，再到解決局部最優(yōu)問題等,，充分體現(xiàn)了本文的創(chuàng)新性技術，為路徑規(guī)劃算法提供了新的研究思路,。實驗結果表明,，該算法切實可行，其搜索效率高,，時間開銷隨路網(wǎng)規(guī)模的擴大增幅較小,，適用于大規(guī)模路網(wǎng)，同時在實時變化的交通路況中更具有實際意義。

參考文獻

　　[1] 岳雙.動態(tài)路徑規(guī)劃算法在車輛導航領域中的應用[J].數(shù)字技術與應用,，2012（3）：95-96.

　　[2] 殷超.基于改進Dijkstra算法的最短路徑搜索仿真[J].山東理工大學學報（自然科學版）,，2011，24（6）：33-36.

　　[3] 張仁平,，周慶忠,，熊偉，等.A*算法改進算法及其應用[J].計算機系統(tǒng)應用,，2009（9）：98-100,，107.

　　[4] 楊易.智能車輛組合定位與路徑導航技術研究[D].長沙：湖南大學，2007.

　　[5] 王健.基于蟻群算法的車輛導航自適應路徑規(guī)劃算法研究[D].青島：青島科技大學,，2011.

　　[6] 于海璁,，陸鋒.一種基于遺傳算法的多模式多標準路徑規(guī)劃方法[J].測繪學報，2014,，43（1）：89-96.

　　[7] 唐小勇,，于飛，潘洪悅.改進粒子群算法的潛器導航規(guī)劃[J].智能系統(tǒng)學報,，2010,，5（5）：443-448.

　　[8] 史輝.車載導航路徑規(guī)劃算法研究[D].鄭州：解放軍信息工程大學，2010.

　　[9] 李淑紅,，張巧榮.二進制粒子群算法在路徑規(guī)劃中的應用[J].計算機工程與設計,，2009，30（21）：4953-4955.

　　[10] 孫海鵬,，翟傳潤,，戰(zhàn)興群，等.基于實時交通信息的動態(tài)路徑規(guī)劃技術[J].微計算機信息,，2007,，23（8-3）：177-178.