摘  要： 針對(duì)傳統(tǒng)的機(jī)器學(xué)習(xí)算法對(duì)不平衡數(shù)據(jù)集的少類分類準(zhǔn)確率不高的問題，基于支持向量機(jī)和模糊聚類,，提出一種不平衡數(shù)據(jù)加權(quán)集成學(xué)習(xí)算法,。首先提出加權(quán)支持向量機(jī)模型（Weighted Support Vector Machine，WSVM）,，該模型根據(jù)不同類別數(shù)據(jù)所占比例的不同,，為各類別分配不同的權(quán)重，然后將WSVM與模糊聚類結(jié)合提出一種新的集成學(xué)習(xí)算法,。將本文提出的算法應(yīng)用于人造數(shù)據(jù)集和UCI數(shù)據(jù)集實(shí)驗(yàn)中,，實(shí)驗(yàn)結(jié)果表明，所提出的算法能夠有效地解決不平衡數(shù)據(jù)的分類問題,，具有更好的分類性能,。

　　關(guān)鍵詞： 不平衡數(shù)據(jù)集；權(quán)值,；支持向量機(jī),；聚類；集成

0 引言

　　不平衡數(shù)據(jù)[1-2]分類問題一直備受關(guān)注,，已成為機(jī)器學(xué)習(xí)領(lǐng)域中的研究熱點(diǎn)?，F(xiàn)實(shí)生活中，存在著許多不平衡數(shù)據(jù)的例子。如：醫(yī)療診斷,、故障檢測(cè)等,。目前，不平衡數(shù)據(jù)分類問題的處理方法主要分為兩類：

　　數(shù)據(jù)層面上,，主要是對(duì)原始數(shù)據(jù)集進(jìn)行處理,，利用少數(shù)類過采樣、多數(shù)類欠采樣等方法使原始數(shù)據(jù)集各類別數(shù)據(jù)個(gè)數(shù)達(dá)到相對(duì)平衡,。過采樣技術(shù)（Synthetic Minority Ove-rsampling Technique,，SMOTE）[3]通過少類樣本和其近鄰樣本的線性關(guān)系獲得新的少類樣本，減少了過擬合現(xiàn)象,，但在生成新樣本時(shí)存在盲目性,，容易出現(xiàn)樣本混疊現(xiàn)象，增加噪音樣本,。單邊選擇欠采樣技術(shù)（One-sided Selection）[4]尋找互為最近鄰的異類樣本對(duì),，并將其中的多類樣本判斷為噪聲點(diǎn)并刪除，但將噪聲點(diǎn)完全刪除,，會(huì)丟失重要的數(shù)據(jù)信息,。

　　算法層面上，主要是對(duì)已有分類算法進(jìn)行改進(jìn)或是設(shè)計(jì)新算法,。趙相彬等人提出基于欠采樣與修正核函數(shù)相結(jié)合的SVM算法[5],，根據(jù)保角變換修正SVM的核函數(shù)，有效地提高了分類準(zhǔn)確率,。Seref等人提出Weighted Relaxed Support Vector Machine（WRSVM）[6],，WRSVM是代價(jià)敏感學(xué)習(xí)和Relaxed SVM（RSVM）的結(jié)合，減少了離群點(diǎn)的影響,。Lin等人提出基于SVM和聚類的不平衡數(shù)據(jù)分類算法[7],，該算法利用模糊聚類（FCM）將訓(xùn)練集的多類數(shù)據(jù)集分成幾個(gè)子集，然后用每個(gè)子集和訓(xùn)練集的少類分別訓(xùn)練子分類器,，最后通過投票原則確定最終分類結(jié)果,。但FCM并不是對(duì)數(shù)據(jù)集平均分組。例如,，設(shè)多類數(shù)據(jù)個(gè)數(shù)為100個(gè),，少類數(shù)據(jù)個(gè)數(shù)為30個(gè)，則需將100個(gè)多類數(shù)據(jù)分為3個(gè)子集,，各子集個(gè)數(shù)可能為（24,，36，40）,、（10,，25,，65），當(dāng)子集個(gè)數(shù)為65時(shí),，和少類數(shù)據(jù)個(gè)數(shù)30相比,，兩類數(shù)據(jù)個(gè)數(shù)依然是不平衡的。

　　因此,，針對(duì)這一問題,，本文提出一種加權(quán)集成學(xué)習(xí)算法——Ensemble Weighted Sup-port Vector Machine based on FCM（FCM-EN WSVM）。首先提出加權(quán)支持向量機(jī)模型,，該模型根據(jù)不同類別數(shù)據(jù)所占比例不同,，為各類別分配不同的權(quán)重。然后利用FCM將訓(xùn)練集的多類數(shù)據(jù)分為若干子集,，每個(gè)子集分別和訓(xùn)練集的少類作為新的訓(xùn)練集訓(xùn)練多個(gè)WSVM分類器,，最后對(duì)測(cè)試集進(jìn)行測(cè)試，通過投票原則確定最終分類結(jié)果,。新算法有效地解決了不平衡數(shù)據(jù)的分類問題,。

1 支持向量機(jī)

　　支持向量機(jī)（Support Vector Machine，SVM）[8-9]是Corinna Cortes和Vapnik等人于1995年首先提出的,，其基本原理：假設(shè)給定帶有標(biāo)簽的訓(xùn)練集S={（x1,，y1）,，…,，（xn，yn）},，其中,，xi∈RN表示樣本點(diǎn)，yi∈{-1,，1}表示所屬類別標(biāo)簽,，i=1，…,，n,。則SVM模型的目標(biāo)函數(shù)為：

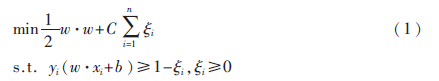
　　其中?孜i為松弛變量，C為懲罰參數(shù),，建立拉格朗日函數(shù),，式（1）轉(zhuǎn)化為其對(duì)偶問題：

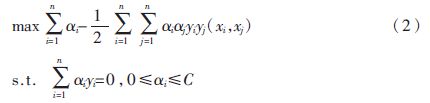
　　則其決策函數(shù)為：

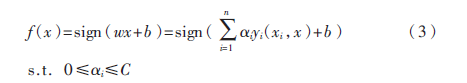
　　在非線性可分情況下，輸入樣本空間找不到最優(yōu)分類超平面,，因此將數(shù)據(jù)通過核函數(shù)映射到高維特征空間中,，此時(shí)：

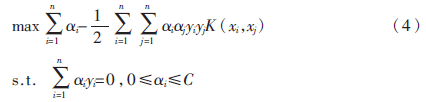
　　其決策函數(shù)為：

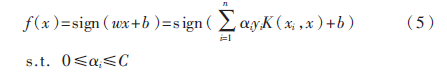
　　2 本文提出的算法

　　2.1 加權(quán)支持向量機(jī)（WSVM）

　　為了減小數(shù)據(jù)類別不平衡對(duì)SVM訓(xùn)練模型的影響，根據(jù)每個(gè)類別數(shù)據(jù)對(duì)分類貢獻(xiàn)的不同,，區(qū)別對(duì)待每一類別數(shù)據(jù),，為其分配不同的權(quán)值,，則WSVM模型的目標(biāo)函數(shù)為：

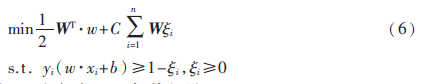
　　其中W為各類別的權(quán)值矩陣。

　　式（6）的對(duì)偶問題為:

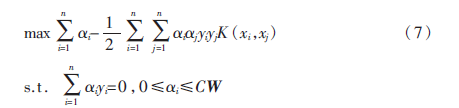
　　那么,，映射到高維空間的決策函數(shù)為：

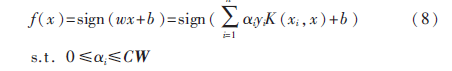
　　2.2 權(quán)值的定義

　　權(quán)值W需滿足以下條件：

　?。?）少類數(shù)據(jù)的權(quán)值大于多類數(shù)據(jù)的權(quán)值，即Wshao>Wduo,；

　?。?）Wi∈（0，1）,，且,，C為數(shù)據(jù)的類別數(shù)。

　　設(shè)訓(xùn)練集的樣本數(shù)為N,，類別數(shù)為C,，各類別的樣本數(shù)從小到大排序依次為n1，n2,，…,，nC，則第i類數(shù)據(jù)的權(quán)值定義為：

　　根據(jù)不同類別樣本個(gè)數(shù)所占的比例為其分配不同的權(quán)重,，多類數(shù)據(jù)的權(quán)重大,，少類數(shù)據(jù)的權(quán)重小，從而使各類別數(shù)據(jù)比例趨于平衡,。

　　2.3 FCM-ENWSVM

　　模糊C均值聚類算法（Fuzzy C-means,，F(xiàn)CM）[10]于1981年被Bezdek提出。它的思想是將數(shù)據(jù)集劃分為不同的簇,，要求同一簇的對(duì)象之間的相似度盡可能的大,，而不同簇的對(duì)象之間的相似度盡可能的小。

　　FCM-ENWSVM算法（基于支持向量機(jī)和聚類的不平衡數(shù)據(jù)加權(quán)集成學(xué)習(xí)算法）：

　?。?）計(jì)算訓(xùn)練集的多類數(shù)據(jù)和少類數(shù)據(jù)的個(gè)數(shù),，并將其個(gè)數(shù)比記為M；

　?。?）利用FCM算法將多類數(shù)據(jù)集分為M個(gè)子集,；

　　（3）M個(gè)子集分別和少類數(shù)據(jù)構(gòu)成新的訓(xùn)練集,，訓(xùn)練M個(gè)WSVM分類器,；

　　（4）分別用M個(gè)分類器對(duì)測(cè)試集進(jìn)行測(cè)試,。

　　最終結(jié)果通過投票原則決定,。

3 實(shí)驗(yàn)結(jié)果及分析

　　3.1 人造數(shù)據(jù)

　　隨機(jī)生成一個(gè)300×2的數(shù)據(jù)集，按3∶1的比例隨機(jī)分為訓(xùn)練集和測(cè)試集,。實(shí)驗(yàn)中,，分別用訓(xùn)練集訓(xùn)練SVM,、WSVM兩種分類器，核函數(shù)選擇文獻(xiàn)[11]中的Linear,、RBF,。圖1、圖2分別表示兩種核函數(shù)的條件下,，兩種分類器對(duì)測(cè)試集的測(cè)試結(jié)果,，其中每幅圖中Original表示測(cè)試集真實(shí)的類別分布，SVM,、WSVM表示用SVM,、WSVM兩種分類器分類后的測(cè)試集類別分布，加號(hào)表示正類（少類）1,，點(diǎn)表示負(fù)類（多類）0,，圈表示錯(cuò)分的數(shù)據(jù)點(diǎn)F。

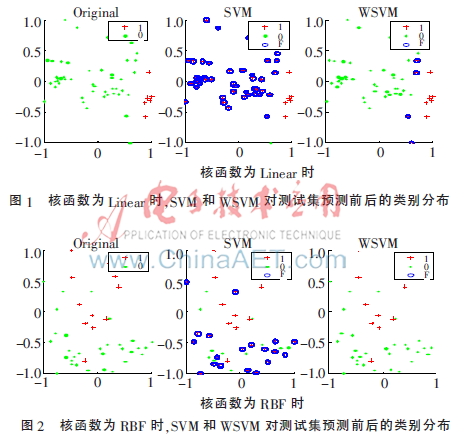
　　從圖1,、圖2可以看出,，在兩種核函數(shù)下，WSVM的分類正確數(shù)都明顯高于SVM的,。WSVM考慮了不同類別數(shù)對(duì)分類準(zhǔn)確率的貢獻(xiàn)多少,，權(quán)值起到了平衡的作用，有效地提高了分類器的性能,。

　　3.2 UCI數(shù)據(jù)實(shí)驗(yàn)

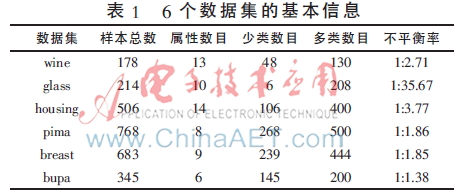
　　從UCI數(shù)據(jù)庫(kù)中選取了6個(gè)數(shù)據(jù)集,，分別為wine、glass,、housing,、pima、breast,、bupa，各數(shù)據(jù)集的基本信息如表1所示,。

　　實(shí)驗(yàn)中,，將表1中的數(shù)據(jù)集按3∶1的比例隨機(jī)分為訓(xùn)練集和測(cè)試集，分類方法選擇SVM,、FSVM[12],、RSVM[11]、FCM-SVM[7],、FCM-ENWSVM（本文算法）,，評(píng)價(jià)準(zhǔn)則選擇文獻(xiàn)[13]中的G-means、F-measure[13],。為了充分驗(yàn)證本文算法的有效性,，圖3,、圖4分別為glass、wine數(shù)據(jù)的訓(xùn)練集打亂順序進(jìn)行8次實(shí)驗(yàn)的結(jié)果折線圖,，表2~表5為其他4個(gè)數(shù)據(jù)集的實(shí)驗(yàn)結(jié)果,，均取循環(huán)20次的平均值。

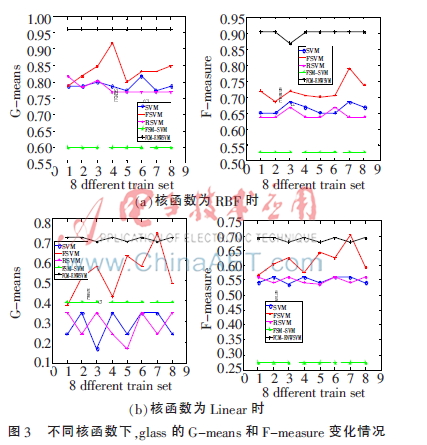
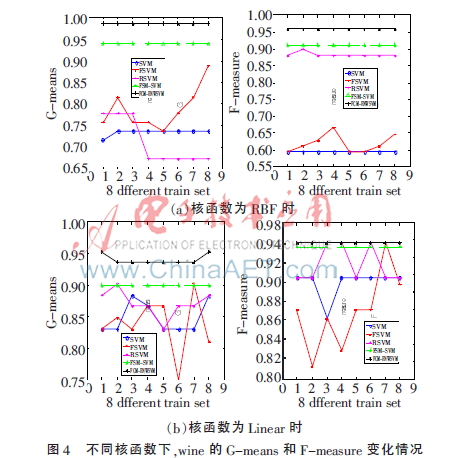
　　從圖3,、圖4可以看出,，本文提出的算法FCM-ENWSVM的G-means和F-measure明顯高于其他方法。FCM-ENWSVM的變化比較穩(wěn)定,，而SVM,、FSVM、RSVM的變化較大,，F(xiàn)CM-SVM雖然比較穩(wěn)定,，但是準(zhǔn)確率低，沒有考慮到FCM不是對(duì)數(shù)據(jù)集進(jìn)行平均分組,，訓(xùn)練集的多類,、少類個(gè)數(shù)依然是不平衡的。然而,，F(xiàn)CM-ENWSVM改進(jìn)了這些算法的不足之處,，通過FCM和權(quán)值改善了數(shù)據(jù)的不平衡性，具有更好的分類效果,。

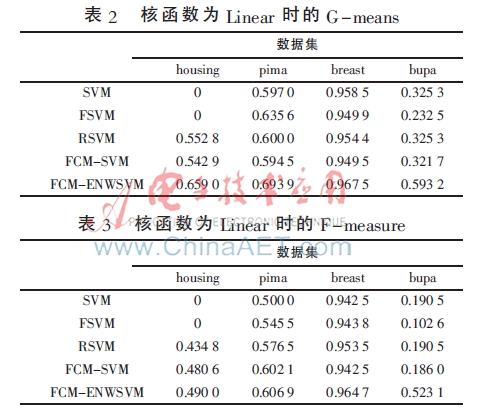
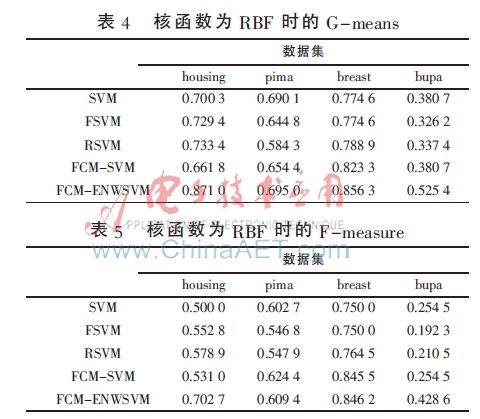
　　從表2~表5中可以看出,，在不同的核函數(shù)下，F(xiàn)CM-ENWSVM的G-means,、F-measure都高于其他方法,。特別地，對(duì)于housing數(shù)據(jù),，當(dāng)核函數(shù)為L(zhǎng)inear時(shí),，SVM、FSVM的G-means,、F-measure都為0,，而FCM-ENWSVM的準(zhǔn)確率相對(duì)較高。還可以發(fā)現(xiàn),，當(dāng)多類少類的不平衡性差時(shí),，如bupa數(shù)據(jù)，SVM和FCM-SVM的結(jié)果相同,，說明在FCM-SVM中,，F(xiàn)CM并沒有起到作用，準(zhǔn)確率依然不高,，而FCM-ENWSVM的卻相對(duì)較高,。FCM-ENWSVM利用了FCM算法,，并考慮到用權(quán)值來改善數(shù)據(jù)的類別不平衡度，從而解決了FCM不平均分組再次造成數(shù)據(jù)不平衡的問題,，有效地提高了分類準(zhǔn)確率,。

4 結(jié)論

　　本文針對(duì)傳統(tǒng)分類算法對(duì)不平衡數(shù)據(jù)的分類準(zhǔn)確率低的問題，基于支持向量機(jī)和模糊聚類,，提出了一種不平衡數(shù)據(jù)加權(quán)集成學(xué)習(xí)算法,。該算法根據(jù)不同類別樣本對(duì)分類貢獻(xiàn)的不同為每個(gè)類別分配不同的權(quán)重，提出加權(quán)支持向量機(jī)模型,，并且利用模糊聚類算法對(duì)訓(xùn)練集的多類數(shù)據(jù)進(jìn)行聚類,，聚類后的每個(gè)子集分別和訓(xùn)練集的少類數(shù)據(jù)作為訓(xùn)練集，訓(xùn)練加權(quán)支持向量機(jī)子分類器,。最后通過投票原則決定最終分類結(jié)果,。將新算法應(yīng)用于實(shí)例數(shù)據(jù)集的分類問題中，有效性和優(yōu)越性得到了證明,。

參考文獻(xiàn)

　　[1] JAPKOW I,， STEPHEN S. The class imbalance problem： a systermatic studay[J]. Intelligent Data Analysis Journal，2002,，6（5）：429-450.

　　[2] YANG Q,，WU X. 10 challenging problems in data mining research[J]. International Journal of Info-rmation Technology&Decision Making，2006,， 5（4）： 597-604.

　　[3] CHAWLA N V,， BOWYER K W， HALL L O,， et al. SMOTE： synthetic minority over-sampling Technique[J]. Journal of Artificial Intelligence Resaerch,， 2002（16）：321-357.

　　[4] KUBAT M， MATWIN S. Addressing the curse of  imbalanced training sets： one-sided selection[C]. Proceedings of the 14th International Conference on Machine Learning,， San Francisco,， 1997：179-186.

　　[5] 趙相彬，梁永全,，陳雪.基于支持向機(jī)的不平衡數(shù)據(jù)分類研究[J].計(jì)算機(jī)與數(shù)字工程,，2013，41（2）：241-243.

　　[6] SEREF O,， RAZZAGHI T， XANTHOPOULOS P. Weighted relaxed support vector machines[J]. Annals of Opearations Research,，Springer US,，2014（9）：1-37.

　　[7] Lin Kaibiao， Weng Wei,， ROBERT K,， et al. Imbalance data classification algorithm based on SVM and clustering function[C]. The 9th International Conference on Computer Science & Education,， 2014：544-548.

　　[8] CORTES C， VAPNIK V. Support-vector networks[J]. Machine Learning,，1995,，20（3）：237-297.

　　[9] VAPNIK V.Statistical learning theory[M]. New York： J.Wiley，1998.

　　[10] BEZDEK J. Pattern recognition with fuzzy objec-tive function algorithms[M]. New York： Plenum press,，1981.

　　[11] 梁紅霞,，閆德勤.粗糙支持向量機(jī)[J].計(jì)算機(jī)科學(xué)，2009,，36（4）：208-210.

　　[12] Huang Hanpang,， Liu Yihung. Fuzzy support vector machines for pattern recognition and data mining[J]. International Journal of Fuzzy Systems， 2002,，4（3）：826-835.

　　[13] 徐麗麗,，閆德勤，高晴.基于聚類欠采樣的極端學(xué)習(xí)機(jī)[J].微型機(jī)與應(yīng)用,，2015,，34（17）：81-84.