周小明1,，陳  剛1，楊宏宇2

　?。?.國網(wǎng)遼寧省電力有限公司,，遼寧 沈陽110006；2.南瑞集團公司信息通信技術分公司,，江蘇 南京210003）

　　摘  要： 本文研究了電力企業(yè)指標的數(shù)據(jù)形態(tài)和業(yè)務形態(tài),，確定指標數(shù)據(jù)在一定時間階段內(nèi)是否穩(wěn)定（業(yè)務是否穩(wěn)定），發(fā)現(xiàn)指標在時間序列的變化特征,，以及觀察指標數(shù)據(jù)在每個時間周期內(nèi)是否呈線性趨勢,，應用統(tǒng)計學及數(shù)據(jù)挖掘方法，結合業(yè)務的精細化需要,，提出了適用于不同特性指標的三種閾值設置方法,，包括正態(tài)分布指標閾值設置方法、時間序列指標閾值設置方法以及線性擬合指標閾值設置方法,。實驗結果表明,，本文提出的三種閾值設置方法能夠反映業(yè)務實際，對國家電網(wǎng)的運營監(jiān)測有著重要意義,。

　　關鍵詞： 數(shù)據(jù)挖掘,；正態(tài)分布；時間序列,；線性擬合,；閾值設置

0 引言

　　國家電網(wǎng)運營監(jiān)測中心對各業(yè)務部門進行指標數(shù)據(jù)監(jiān)測的主要根據(jù)是業(yè)務專家知識和經(jīng)驗[1-2]，所以對專家的業(yè)務水平有很大的依賴性。本文將數(shù)據(jù)挖掘的方法引入到電力企業(yè)指標閾值設置的研究領域,，用時間序列模型反映數(shù)據(jù)時間變化特征[3-5],，用正態(tài)分布反映數(shù)據(jù)的穩(wěn)定性[6-7]，用線性擬合體現(xiàn)數(shù)據(jù)的線性變化趨勢[8],，在一定程度上解決了以往設置的閾值缺少客觀依據(jù)的現(xiàn)狀,。

1 指標閾值設置方法

　　本文介紹了三種指標閾值設置方法，包括正態(tài)分布方法,、時間序列方法,、線性擬合方法，其中涉及到的正態(tài)分布有效性檢驗,、時間序列建模條件檢驗和模型創(chuàng)建,，以及線性擬合均采用工具Pluto數(shù)據(jù)挖掘平臺實現(xiàn),。

　　1.1 正態(tài)分布

　　1.1.1 正態(tài)分布算法介紹

　　正態(tài)分布是實踐中應用最為廣泛,、在理論上研究最多的分布之一，它在概率統(tǒng)計中占用特別重要的地位,。

　　正態(tài)分布的概率密度函數(shù)為：

　　正態(tài)分布的3規(guī)則如圖1所示,，置信區(qū)間如表1。

　　1.1.2 正態(tài)分布指標閾值設置方法

　　正態(tài)分布指標閾值設置方法,，首先需要判斷指標數(shù)據(jù)是否符合正態(tài)分布,，若符合正態(tài)分布，則選取最近周期的指標數(shù)據(jù)作為分析對象,，計算該樣本數(shù)據(jù)的均值與標準差,，根據(jù)正態(tài)分布置信區(qū)間的覆蓋率，結合業(yè)務的精細化需要,，上下限圍繞中心點（均值）做2個標準差的波動形成指標閾值,。

　　1.1.3 適用于正態(tài)分布閾值設置方法的指標特性

　　(1)在一段較長時間周期內(nèi)（1年以上），業(yè)務是穩(wěn)定的,、收斂的,。數(shù)據(jù)呈現(xiàn)出來的形式是趨近與某一點，并在一定范圍內(nèi)波動,。

　　(2)在正態(tài)分布有效性檢驗中P值>0.05時,，說明樣本數(shù)據(jù)符合正態(tài)分布形態(tài)。

　　(3)適用于服從正態(tài)分布的數(shù)據(jù),。

　　(4)受連續(xù)時間因素干擾較小,。

　　1.2 時間序列

　　1.2.1 時間序列算法介紹

　　時間序列法是一種定量預測方法，在數(shù)據(jù)挖掘中作為一種常用的預測手段被廣泛應用,。對時間序列建模的兩個任務,，一是分析當期數(shù)據(jù)如何受前幾期的數(shù)據(jù)影響，二是變量在時間變化上的規(guī)律性。

　　本文選用的時間序列算法為ARIMA算法,。

　　ARIMA模型是將非平穩(wěn)時間序列轉化為平穩(wěn)時間序列,，然后將因變量僅對它的滯后值以及隨機誤差項的現(xiàn)值和滯后值進行回歸所建立的模型。在ARIMA模型的識別過程中,，主要用到兩個工具：一是自相關函數(shù)(簡稱ACF）,，二是偏自相關函數(shù)(簡稱PACF)以及它們各自的相關圖（即ACF、PACF相對于滯后長度描圖）,。對于一個序列y來說,，它的第k階自相關系數(shù)(記作rk)定義為它的k階自協(xié)方差除以它的方差。

　　它是關于k的函數(shù),，因此也稱之為自相關函數(shù),，通常記為ACF(k)。偏自相關函數(shù)PACF(k)度量了消除中間滯后項影響后兩滯后變量之間的相關關系,。

　　ARIMA(p,，d，q)模型是經(jīng)過d階差分變換后的ARMA(p,，q)模型,，ARMA(p，q)模型的一般形式：

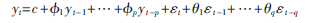
　　ARIMA(p,，d,，q)模型的算法如下：

　　(1)對原序列進行平穩(wěn)性檢驗，如果序列不滿足平穩(wěn)性條件,，可以通過差分變換（單整階數(shù)為d,，則進行d階差分）或者其他變換，如對數(shù)差分變換使序列滿足平穩(wěn)性條件,。

　　(2)通過計算能夠描述序列特征的一些統(tǒng)計量（如自相關系數(shù)和偏自相關系數(shù)）,，來確定ARMA模型的階數(shù)p和q，并在初始估計中選擇盡可能少的參數(shù),。

　　(3)估計模型的未知參數(shù),，并檢驗參數(shù)的顯著性，以及模型本身的合理性,。

　　(4)進行診斷分析,，以證實所得模型確實與所觀察到的數(shù)據(jù)特征相符。

　　1.2.2 時間序列指標閾值設置方法

　　時間序列指標閾值設置方法,，首先需要對時間上連續(xù)的指標數(shù)據(jù)進行時間序列建模條件檢驗,，如果數(shù)據(jù)既滿足平穩(wěn)性，又具有相關性,，則應用ARIMA算法對樣本數(shù)據(jù)進行ARIMA時間序列建模,，對模型性能進行評估,，若模型可用，則以模型創(chuàng)建過程中形成的樣本預測數(shù)據(jù)與實際數(shù)據(jù)的偏差為分析對象,，計算其誤差均值與誤差標準差,，根據(jù)正態(tài)分布置信區(qū)間與樣本覆蓋率的對照關系，結合業(yè)務的精細化需要,，上下限圍繞指標當前預測值做2個標準差的波動形成指標閾值,。

　　1.2.3 適用于時間序列閾值設置方法的指標特性

　　(1)當指標數(shù)據(jù)或者一階差分平穩(wěn)性檢驗<0.05，且檢驗模型中數(shù)據(jù)存在自相關和偏自相關性（相關性檢測圖中,，存在自相關系數(shù),、偏自相關系數(shù)超出±2倍估計標準差）時，說明樣本數(shù)據(jù)適合時間序列算法,。

　　(2)適用于連續(xù)時間點數(shù)據(jù)序列,，當數(shù)據(jù)因為數(shù)據(jù)質量出現(xiàn)缺值時應對數(shù)據(jù)進行預處理后才能使用時間序列。

　　(3)不適用與在連續(xù)時間序列中出現(xiàn)多個異常點的情況,。

　　1.3 線性擬合

　　1.3.1 線性擬合算法介紹

　　若兩組數(shù)據(jù)X和Y具有統(tǒng)計關系而且是線性關系,，那么就可以建立回歸模型：

　　。

　　1.3.2 線性擬合指標閾值設置方法

　　線性擬合指標閾值設置方法是,，首先需要觀察指標歷史數(shù)據(jù)的變化趨勢,，如果數(shù)據(jù)在每個時間周期內(nèi)呈線性趨勢，并且不同時間周期數(shù)據(jù)的變化趨勢近似相同,，則對每個時間周期內(nèi)的數(shù)據(jù)分別應用線性擬合算法進行一元線性回歸，若擬合度R2都大于0.95,，則選擇最近時間周期內(nèi)的數(shù)據(jù)及線性擬合函數(shù),，以該樣本預測數(shù)據(jù)與實際數(shù)據(jù)的偏差為分析對象，計算其誤差均值與誤差標準差,，按正態(tài)分布置信區(qū)間與樣本覆蓋率的對照關系,，結合業(yè)務的精細化需要，上下限圍繞指標當前預測值做3個標準差的波動形成指標閾值,。

　　1.3.3 適用于線性擬合閾值設置方法的指標特性

　　(1)在每個時間周期（一般選擇1年為一個周期）內(nèi),，業(yè)務是穩(wěn)定的。數(shù)據(jù)在每個時間周期內(nèi)呈線性趨勢,，并且不同時間周期數(shù)據(jù)的變化趨勢近似相同（即不同時間周期內(nèi)同一時間點的指標值幾乎相同）,。比較適用于指標的累計值。

　　(2)對每個時間周期內(nèi)的數(shù)據(jù)進行線性擬合,，擬合度R2都需大于0.95,。

　　(3)適用于具有線性趨勢的數(shù)據(jù)。

　　(4)受連續(xù)時間因素干擾較小,。

2 實驗結果及分析

　　本次實驗在選取數(shù)據(jù)時,，依據(jù)運營監(jiān)測指標體系中的指標項,，采用某省電力公司的3個指標的省數(shù)據(jù)作為研究對象，運用以上介紹的三種指標閾值設置方法進行實驗分析,。指標清單如表2,。

　　2.1 基于正態(tài)分布方法的“總資產(chǎn)周轉率”閾值設置

　　2.1.1 指標數(shù)據(jù)進行正態(tài)分布分析

　　選取總資產(chǎn)周轉率當期值，2012年1月到2012年12的樣本數(shù)據(jù)進行正態(tài)性分布檢測,，共計12條數(shù)據(jù),。利用正態(tài)分布校驗模型分析，其顯著性指標P=0.754,，P值大于0.05,，說明服從正態(tài)分布。校驗圖如圖2,。

　　2.1.2 波動區(qū)間計算

　　以正態(tài)分布置信區(qū)間與分布覆蓋率對照表為依據(jù),，以保證95%的樣本值落入域值范圍作為異動監(jiān)測要求。

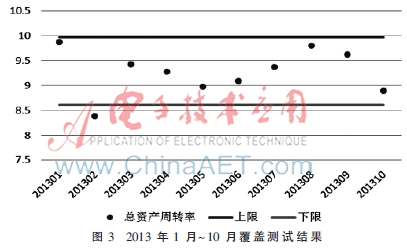
　　利用正態(tài)分布統(tǒng)計分析模型,，計算所提供的2012年的12條樣本數(shù)據(jù)的均值與標準差,。均值為：9.291，標準差為：0.339,，按上下限圍繞中心點做2個標準差的波動形成指標閾值,。可計算得到總資產(chǎn)周轉率上限為：9.970,，下限為：8.613,。

　　按照上述2012年數(shù)據(jù)得到的閾值，對2013年1月到10月數(shù)據(jù)（共10條數(shù)據(jù)）進行覆蓋率測試,，如圖3所示,。

　　2.2 基于時間序列方法的“單位購電成本”閾值設置

　　選取單位購電成本當前值，2008年1月到2013年9月省數(shù)據(jù),，共計69條數(shù)據(jù)（其中,，2013年3月和4月數(shù)據(jù)為空）。以2008年1月～2013年2月的數(shù)據(jù)為時間序列模型使用的樣本數(shù)據(jù),，包括模型構建樣本數(shù)據(jù)（2008年1月～2012年12月的數(shù)據(jù)）與測試數(shù)據(jù)（2013年1月和2月的數(shù)據(jù)）,，共計62條記錄。

　　2.2.1 樣本數(shù)據(jù)檢驗

　　(1)數(shù)據(jù)的平穩(wěn)性檢驗

　　應用檢驗模型得到P=0.951 5,，說明該數(shù)據(jù)是一組非平穩(wěn)序列,。

　　對原數(shù)據(jù)進行一階差分處理，對差分后的數(shù)據(jù)再次進行平穩(wěn)性檢驗,，P=0.000 0,，此時數(shù)據(jù)具有平穩(wěn)性。說明原數(shù)據(jù)具有一階平穩(wěn)性,。

　　(2)數(shù)據(jù)的相關性檢驗

　　對一階差分后的數(shù)據(jù)進行相關性檢驗,，具有相關性（包括自相關和偏自相關）,。相關性檢驗如圖4所示。

　　從檢驗結果可以看出,，此時數(shù)據(jù)存在自相關和偏自相關性（相關性檢測圖中,，序列1階自相關系數(shù)、1階偏自相關系數(shù)均比較顯著,，具有自相關性）,。因此，該數(shù)據(jù)可進行時間序列建模,。

　　2.2.2 時間序列建模

　　選取2008年1月～2012年12月的數(shù)據(jù)作為時間序列建模的訓練樣本,，2013年1月和2月的數(shù)據(jù)作為測試樣本。時間序列如圖5所示,。

　　以ARIMA時間序列模型為預測模型,，獲得2013年1月和2月時間序列預測結果與實際數(shù)據(jù)比對誤差如表3。

　　2.2.3 波動區(qū)間計算

　　上述時間序列模型的誤差的均值為0.139 2,，誤差的標準差為：6.520 4,。應用時間序列模型，實時地預測2013年1月～2013年9月各月單位購電成本,。并根據(jù)設置指標波動區(qū)間的方法,，設置各月指標的閾值區(qū)間，如表3,。

　　2.3 基于線性擬合方法的“累計總資產(chǎn)周轉率”閾值設置

　　2.3.1 指標數(shù)據(jù)線性擬合分析

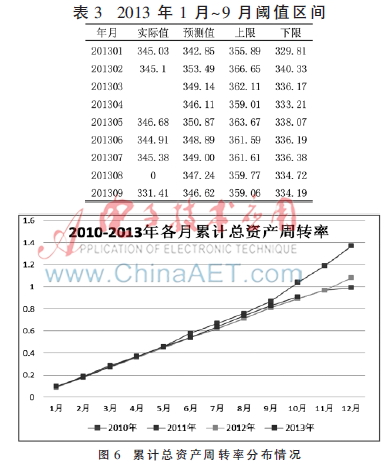
　　選取總資產(chǎn)周轉率累計值,，2010年1月～2013年10月省數(shù)據(jù)，共46條,。該指標數(shù)據(jù)在一年內(nèi)（12個月）呈線性增長的趨勢,，并且每年的變化趨勢近似相同。2010年～2013年各月數(shù)據(jù)的分布情況如圖6所示,。

　　對2010年、2011年,、2012年的數(shù)據(jù)（每年12條數(shù)據(jù)）分別按照月份進行線性擬合,，2010年、2011年,、2012年的數(shù)據(jù)線性擬合的擬合優(yōu)度均大于0.95,，說明“總資產(chǎn)周轉率”指標的累計值在一年內(nèi)呈線性增長趨勢，并且在每年的同月指標值幾乎相同,。

　　2.3.2 波動區(qū)間計算

　　選取2012年各月數(shù)據(jù)得到線性擬合函數(shù),，計算2012年各月的預測值，同時以該樣本數(shù)據(jù)的預測值與實際數(shù)據(jù)的偏差為分析對象,，計算其誤差均值與標準差,。

　　經(jīng)計算得到誤差的均值為0.000 258,，誤差的標準差為：0.005 931。應用以上線性擬合函數(shù),，預測2013年1月～2013年10月遼寧各月累計總資產(chǎn)周轉率值,，并根據(jù)設置指標波動區(qū)間的方法，設置各月指標的閾值區(qū)間,。

　　3 結論

　　本文根據(jù)國家電網(wǎng)的運營監(jiān)測中心對于指標的監(jiān)測有較多指標閾值設置是由業(yè)務專家人工設置實現(xiàn)的現(xiàn)狀,，針對存在部分指標設置沒有結合各地區(qū)業(yè)務能力的差異，或者沒有充分考慮業(yè)務自身規(guī)律等問題,，通過研究指標的數(shù)據(jù)形態(tài)和業(yè)務形態(tài),，確定指標數(shù)據(jù)在一定時間階段內(nèi)是否穩(wěn)定（業(yè)務是否穩(wěn)定），發(fā)現(xiàn)指標在時間序列的變化特征,，以及觀察指標數(shù)據(jù)在每個時間周期內(nèi)是否呈線性趨勢,，結合統(tǒng)計學及數(shù)據(jù)挖掘方法，提出了適用于不同特性指標的三種閾值設置方法——時間序列指標閾值設置方法,、正態(tài)分布指標閾值設置方法以及線性擬合指標閾值設置方法,。在此基礎上，應用本文提出的方法對相適用三類指標進行了實驗和分析,，并將通過線性擬合方法得到的“累計總資產(chǎn)周轉率”的閾值和目前國網(wǎng)已有的閾值進行了對比實驗,。實驗結果表明本文的方法設置的指標閥值更加合理，更能反映客觀現(xiàn)實情況,。

　　參考文獻

　　[1] 張云飛.我國電力行業(yè)運行情況剖析[J].上海電力,，2008(6)：519-524.

　　[2] 國家電網(wǎng)公司總部運營監(jiān)測(控)中心建成投運[J].電力信息化，2013(6)：111-112.

　　[3] 段江嬌.基于模型的時間序列數(shù)據(jù)挖掘[D].上海：復旦大學,，2008.

　　[4] 谷赫.時間序列的數(shù)據(jù)挖掘在證券預測分析中的應用研究[D].長春：吉林大學,，2005.

　　[5] 李慶雷，馬楠,，付遵濤.時間序列非平穩(wěn)檢測方法的對比分析[J].北京大學學報(自然科學版),，2013(2)：252-260.

　　[6] 馬莉.電力市場環(huán)境下發(fā)電公司報價策略研究[D].杭州：浙江大學，2003.

　　[7] 杜宇上.基于正態(tài)密度函數(shù)的滾動窗口路徑規(guī)劃方法[J].科學技術與工程,，2010(15)：3741-3744.

　　[8] 何菊明,，王芙.實驗數(shù)據(jù)的線性擬合及計算機處理[J].武漢工程大學學報，2008,，30(1)：117-119.