0 引言

    自抗擾控制器（Active disturbance rejection controller）是一種非線性控制器^[1],，該控制器將系統(tǒng)模型的內(nèi)部擾動(dòng)和外部擾動(dòng)看為總擾動(dòng)，通過(guò)擴(kuò)張觀測(cè)器對(duì)總擾動(dòng)進(jìn)行估計(jì)和補(bǔ)償,。因此,，ADRC可以有效解決一些非線性不確定系統(tǒng)的控制問(wèn)題^[2-3],。相對(duì)于非線性自抗擾控制器，線性自抗擾控制器設(shè)計(jì)簡(jiǎn)單,，控制器參數(shù)調(diào)節(jié)有相對(duì)確定的方法^[4],。ADRC是否能充分發(fā)揮其性能依賴于控制器的參數(shù)設(shè)置是否最優(yōu)。ADRC需要優(yōu)化的參數(shù)較多,，若依靠經(jīng)驗(yàn)調(diào)試線性ADRC的參數(shù)，非常耗時(shí),，且無(wú)法保證系統(tǒng)響應(yīng)最優(yōu)或次優(yōu),。文獻(xiàn)[5]采用各種算法對(duì)線性自抗擾控制器多參數(shù)整定問(wèn)題進(jìn)行調(diào)優(yōu)。但這些方法復(fù)雜,，實(shí)際應(yīng)用有一定難度,。

    PSO算法在算法早期迭代時(shí)的效果很好，但在鄰近最優(yōu)解時(shí)出現(xiàn)了停滯,。DE算法的多樣性及搜索能力的魯棒性較強(qiáng),，但后期收斂速度較慢。針對(duì)這個(gè)問(wèn)題,，本文提出一種PSODE混合優(yōu)化計(jì)算方法,。新算法的前期基于慣性權(quán)重改進(jìn)策略有效擴(kuò)大搜索步長(zhǎng)，粒子大范圍搜索,。當(dāng)PSO的搜索停滯時(shí),，對(duì)pbest空間進(jìn)行變異同時(shí)自適應(yīng)調(diào)整粒子搜索步長(zhǎng)，既避免了算法出現(xiàn)早熟問(wèn)題增加粒子的多樣性,，又利于粒子加速收斂,，保證尋優(yōu)速度。本文采用該算法應(yīng)用于優(yōu)化線性自抗擾控制器的參數(shù),，并進(jìn)行了仿真研究,，結(jié)果表明可以有效提高系統(tǒng)的控制性能。

1 線性ADRC控制器

    二階線性ADRC控制器的結(jié)構(gòu)圖如圖1所示,。圖中y和r是控制器輸出和參考輸入信號(hào),。u為控制量，d為未知外擾,，Gp是被控對(duì)象,。ESO（Extended State Observer）為擴(kuò)張狀態(tài)觀測(cè)器。

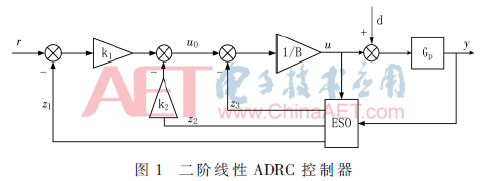
    二階線性ADRC中ESO的一般形式：

2 PSODE混合算法

2.1 標(biāo)準(zhǔn)PSO算法

    粒子群優(yōu)化算法是一種收斂速度快,、算法簡(jiǎn)單的全局優(yōu)化進(jìn)化算法,。pbest和gbest分別表示粒子的最優(yōu)位置和群體的最優(yōu)位置，可以把它們看成PSO算法的兩個(gè)輸入,。PSO算法中,，隨著迭代次數(shù)增加,，粒子的多樣性會(huì)逐漸減小，這增加了陷入局部最優(yōu)的可能性,。

2.2 標(biāo)準(zhǔn)DE算法

    DE算法首先在搜索范圍內(nèi)隨機(jī)生成粒子,，再采用變異、交叉,、選擇三大步驟來(lái)更新種群,，其更新過(guò)程與遺傳算法類似。

    因?yàn)镈E含有變異屬性和交叉屬性,，所以相比PSO,，DE算法全局搜索性能更好一些。但是,，這種變異性可能帶來(lái)收斂速度慢的問(wèn)題,，導(dǎo)致局部搜索性能降低。

2.3 慣性權(quán)重改進(jìn)策略

    權(quán)重系數(shù)的取值研究是改進(jìn)PSO算法的重點(diǎn),。根據(jù)粒子與當(dāng)前種群最優(yōu)值的平均距離和粒子與當(dāng)前種群的最大距離對(duì)慣性權(quán)重進(jìn)行改進(jìn),。

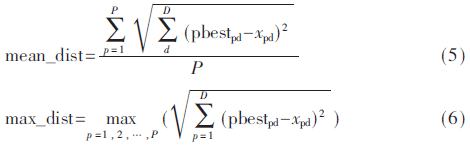
    距離變化率的定義為:

    k的取值隨著粒子與當(dāng)前種群最優(yōu)值的平均距離和粒子與當(dāng)前種群的最大距離變小而變小，表明需要提高它的精細(xì)搜索能力,，反之,，則需要提高它的全局搜索能力。η的取值：

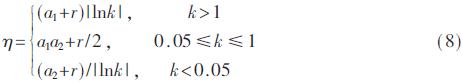
其中,，a₁=0.3,，a₂=0.2，r為[0,，1]間均勻分布的隨機(jī)數(shù),，η的值隨迭代次數(shù)的變化而變化，可以提高前期粒子搜索范圍和粒子后期的搜索精度,。

2.4 PSODE混合策略

    本文提出了PSODE混合算法,，DE算法中的變異性可以為粒子提供更好的多樣性，本文為pbest和gbest兩項(xiàng)提供變異差分性能,，確保全局搜索能力,。混合策略有兩個(gè)條件：(1)當(dāng)PSO算法中L百分比的種群出現(xiàn)停滯現(xiàn)象,。(2)如果這些點(diǎn)連續(xù)停滯S次,，若滿足條件則異步間歇性調(diào)用R次DE算法，混合策略如圖2所示,。

    根據(jù)以上分析,，PSODE算法步驟如下：

    步驟(1)：初始化種群，輸入算法各參數(shù),。

    步驟(2)：計(jì)算粒子適應(yīng)度,，得到初始個(gè)體極值x^pbest(k),，p=1，…,，P和全體極值x^gbest(k),。

    步驟(3)：對(duì)粒子群位置和速度進(jìn)行更新，計(jì)算適應(yīng)度,，更新個(gè)體極值x^pbest(k),，p=1，…,，P和全體極值x^gbest(k),。

    步驟(4)：檢查混合調(diào)用條件，如果L個(gè)pbest的搜索點(diǎn)保持不變,，且連續(xù)停滯S次，那么異步間歇性調(diào)用R次混合算法,。若滿足調(diào)用條件,，跳到步驟(5)，否則進(jìn)行步驟(8),。

    步驟(5)：在個(gè)體極值x^pbest(k),，p=1，…,，P中隨機(jī)取3個(gè)互不相同的粒子r₁,、r₂、r₃,，對(duì)其采取變異策略得到y(tǒng)^L(k),。

    步驟(6)：對(duì)變異后的粒子進(jìn)行交叉。

    步驟(7)：選取較小適應(yīng)度值的位置作為pbest,，并更新gbest的位置,。DE調(diào)用次數(shù)小于R時(shí)回到步驟(5)，否則進(jìn)行步驟(8),。

    步驟(8)：若滿足結(jié)束條件,，輸出gbest，算法終止,，否則返回步驟(3),。

3 基于PSODE算法的ADRC控制器設(shè)計(jì)

3.1 適應(yīng)度函數(shù)的選擇

    本文選用ITAE值作為一個(gè)子項(xiàng)來(lái)評(píng)價(jià)系統(tǒng)的動(dòng)態(tài)性能，將上升時(shí)間t_r,、超調(diào)量σ,、控制能量u以不同的形式綜合到評(píng)價(jià)函數(shù)中。系統(tǒng)輸出信號(hào)達(dá)到目標(biāo)值后不僅會(huì)有超調(diào),，也有可能產(chǎn)生信號(hào)回撤,，為了防止系統(tǒng)信號(hào)回撤較大,，加入懲罰因子λ₅。性能評(píng)價(jià)函數(shù)如式(9)所示,。

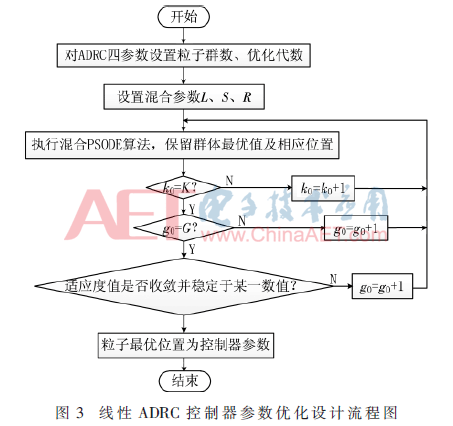
3.2 PSODE混合算法流程

    適應(yīng)度函數(shù)被確定后,，對(duì)控制器的參數(shù)進(jìn)行尋優(yōu)。在滿足約束條件的前提下,，適應(yīng)度函數(shù)的數(shù)值達(dá)到最小時(shí)所對(duì)應(yīng)的參數(shù)為最優(yōu)參數(shù),。PSODE算法優(yōu)化線性ADRC控制器問(wèn)題的優(yōu)化設(shè)計(jì)流程圖如圖3所示。

4 鍋爐過(guò)熱氣溫系統(tǒng)的仿真實(shí)驗(yàn)

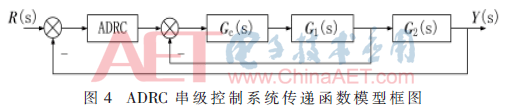
    以文獻(xiàn)[7]負(fù)載為75%工況為例,，采用串級(jí)控制系統(tǒng)對(duì)其進(jìn)行設(shè)計(jì),。圖4為串級(jí)控制系統(tǒng)的結(jié)構(gòu)框圖。

    副回路比例值為100,。首先用交叉兩點(diǎn)法對(duì)被控回路進(jìn)行降階,，得到一階滯后近似模型：

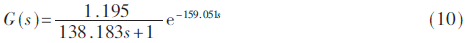
    根據(jù)文獻(xiàn)[8]，設(shè)計(jì)H無(wú)窮非脆弱魯棒PID控制器,，得到PID控制器參數(shù)為：K_P=0.908,，K_I=0.004 3，K_D=45,。

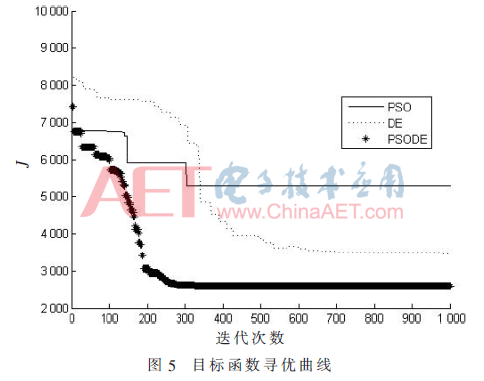
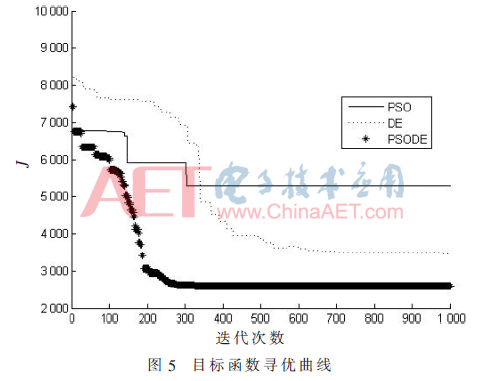
    B取被控對(duì)象傳遞函數(shù)分子部分的零階系數(shù)為1.195,。根據(jù)文獻(xiàn)[9]將PID參數(shù)轉(zhuǎn)化為ADRC參數(shù)，得到需要整定的4個(gè)參數(shù)的初始值,，通過(guò)本文提出的PSODE算法與DE和PSO算法分別對(duì)這4個(gè)參數(shù)的取值進(jìn)行尋優(yōu),。目標(biāo)函數(shù)J的優(yōu)化過(guò)程曲線如圖5所示。從圖中可以看出隨著迭代次數(shù)的增加,，PSODE較其他兩種算法有更快的收斂速度,，且沒(méi)有陷入局部最優(yōu)，最終收斂找到了最優(yōu)解,。

4.1 階躍響應(yīng)仿真

    經(jīng)過(guò)3種算法優(yōu)化后的ADRC參數(shù)如表1所示,。給不同參數(shù)下的控制系統(tǒng)輸入階躍信號(hào)，其系統(tǒng)輸出信號(hào)如圖6所示,。

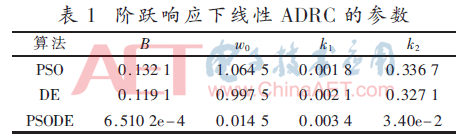
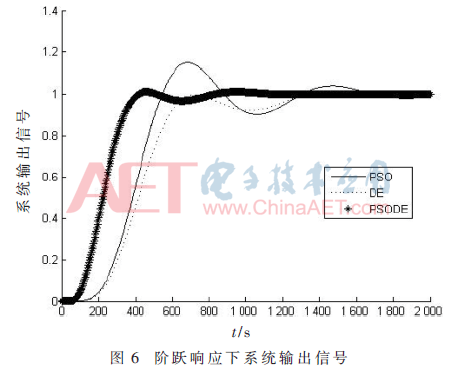
    由圖6可以看出,，基于PSODE優(yōu)化的線性ADRC系統(tǒng)反應(yīng)速度最快，幾乎沒(méi)有超調(diào),，控制效果最更好,。

4.2 魯棒穩(wěn)定性分析

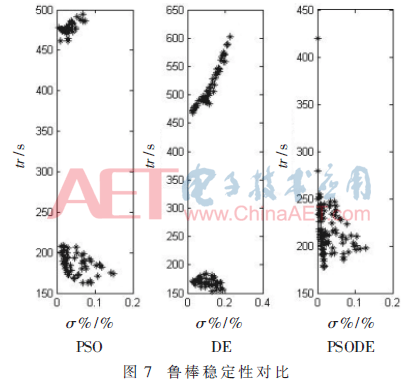
    采用Monte-Carlo隨機(jī)試驗(yàn)方法評(píng)價(jià)控制系統(tǒng)性能魯棒性。令控制器參數(shù)發(fā)生±10%的隨機(jī)變化,，計(jì)算tr,、σ%性能指標(biāo)，重復(fù)仿真100次,。

    圖7中動(dòng)態(tài)分布點(diǎn)是一個(gè)二維向量的集合,，點(diǎn)越集中說(shuō)明性能魯棒性越好,。由圖7可以看出，PSODE下的點(diǎn)分布較為集中且超調(diào)較少,，基于PSODE優(yōu)化的控制系統(tǒng)比另外兩種系統(tǒng)具有更強(qiáng)的魯棒性,。

5 結(jié)論

    針對(duì)自抗擾控制過(guò)程中存在的最優(yōu)參數(shù)難以確定的問(wèn)題，在對(duì)PSODE混合算法和自抗擾控制理論深入研究的基礎(chǔ)上,，提出了基于PSODE 算法的自抗擾控制器優(yōu)化設(shè)計(jì),。提出的帶懲罰策略的評(píng)價(jià)函數(shù)在混合PSODE算法的框架下，可以更快地計(jì)算出控制器參數(shù),，尋優(yōu)精度,、收斂效果和穩(wěn)定性等方面相對(duì)于傳統(tǒng)的算法均得到了很大的提高。同時(shí)也驗(yàn)證了本文提出的算法加強(qiáng)了控制系統(tǒng)的魯棒性,，提高了控制系統(tǒng)的控制能力,。

參考文獻(xiàn)

[1] 韓京清.從PID技術(shù)到“自抗擾控制”技術(shù)[J].控制工程，2002(3)：13-18.

[2] LI D,，LI C,，GAO Z，et al.On active disturbance rejection in temperature regulation of the proton exchange membrane fuel cells[J].Journal of Power Sources,，2015，283：452-463.

[3] TANG H,，LI Y.Development and active disturbance rejection control of a compliant micro-/nanopositioning piezostage with dual mode[J].IEEE Transactions on Industrial Electronics,，2014，61(3)：1475-1492.

[4] GAO Z.Scaling and parameterization based controller tuning[C].Proc.of the 2003 American Control Conference,，2003：4989-4996.

[5] ZHANG Y,，F(xiàn)AN C，ZHAO F,，et al.Parameter tuning of ADRC and its application based on CCCSA[J].Nonlinear Dynamics,，2014，76(2)：1185-1194.

[6] LI D,，GAO Z,，CHEN X，et al.Tuning method for second-order active disturbance rejection control[C].中國(guó)自動(dòng)化學(xué)會(huì)控制理論專業(yè)委員會(huì)D卷,，2011：6322-6327.

[7] Xia Yuanqing,，Liu Bo，F(xiàn)u Mengyin.Active disturbance rejection control for power plant with a single loop[J].Asian Journal of Control,，2012,，14(1)：239-250.

[8] 恒慶海，魯婧,，恒慶珠,，等.紙張定量系統(tǒng)H∞非脆弱魯棒控制器設(shè)計(jì)[C].第二十九屆中國(guó)控制會(huì)議論文集,，2010.

[9] ZHAO C，LI D.Control design for the SISO system with the unknown order and the unknown relative degree[J].Isa Transactions,，2013,，53(4)：858-872.