張家生,崔鵬鵬，沈忱,，韓迎鴿

　?。ò不绽砉ご髮W(xué) 電氣與信息工程學(xué)院,安徽 淮南 232001）

　　摘要：針對(duì)基于CMA的DFE盲均衡算法收斂速度慢、收斂后穩(wěn)態(tài)剩余誤差大的缺點(diǎn),提出了一種改進(jìn)的基于CMA的DFE盲均衡算法,。該算法通過引入均方誤差作為調(diào)整步長(zhǎng)的參量,，構(gòu)造出指數(shù)型變步長(zhǎng)函數(shù)，把基于CMA的DFE盲均衡算法中前饋濾波器和反饋濾波器更新方程中的固定步長(zhǎng)值變?yōu)榭勺冎?，并?duì)其收斂性做了分析,。計(jì)算機(jī)仿真表明，改進(jìn)算法具有較快的收斂速度和更小的剩余誤差,。

　　關(guān)鍵詞：CMA,；碼間干擾（ISI）；判決反饋均衡器（DFE）,；變步長(zhǎng)

　　中圖分類號(hào)：TN911文獻(xiàn)標(biāo)識(shí)碼：ADOI： 10.19358/j.issn.1674-7720.2017.09.021

　　引用格式：張家生,崔鵬鵬,，沈忱，等.一種改進(jìn)的變步長(zhǎng)常模判決反饋盲均衡算法［J］.微型機(jī)與應(yīng)用,，2017,36（9）：71-73,，77.

0引言

　　高速數(shù)據(jù)通信系統(tǒng)中,碼間干擾是影響通信質(zhì)量的主要決定因素，為了消除碼間干擾(Inter Symbol Interference, ISI),必須進(jìn)行信道均衡,。盲均衡由于不需要發(fā)送訓(xùn)練序列引起了各國(guó)學(xué)術(shù)界以及通信業(yè)界的高度重視,。在各種盲均衡算法中，基于常數(shù)模算法（Constant Modulus Algorithm,CMA)的判決反饋盲均衡（Decision Feedback Equalization,DFE）由于反饋濾波器部件具有非線性特性,，能在有效消除ISI的同時(shí)不引入增益噪聲［12］,，因此得到了廣泛應(yīng)用。但是在許多情況下相對(duì)于CMA,，DFE的收斂速度和穩(wěn)態(tài)性能改善得并不明顯,，尤其在信號(hào)的模值不是常數(shù)的情況下,。這是因?yàn)榛贑MA的DFE采用的是固定步長(zhǎng)的常數(shù)模算法，而對(duì)于非常模信號(hào),，在星座圖中的任何一個(gè)信號(hào)都無法使CMA的代價(jià)函數(shù)為零,，因此基于CMA的DFE就會(huì)發(fā)生過調(diào)，導(dǎo)致收斂慢,，收斂后穩(wěn)態(tài)誤差較大［34］,。

　　為了提高基于CMA的DFE的收斂速度，減小穩(wěn)態(tài)誤差,，本文提出一種改進(jìn)的基于CMA的DFE盲均衡算法,該算法通過引入均方誤差作為調(diào)整步長(zhǎng)的參量,，把基于CMA的DFE盲均衡算法中前饋濾波器和反饋濾波器更新方程中的固定步長(zhǎng)值變?yōu)榭勺冎担云讷@得較好的均衡效果和收斂性能,。

1基于CMA的DFE算法

　　基于CMA的DFE算法由一個(gè)前饋濾波器和一個(gè)反饋濾波器組成,，其中反饋濾波器由判決裝置輸出的判決驅(qū)動(dòng)，其原理圖如圖1所示,。

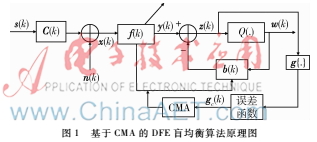
　　圖1中,，s(k)是獨(dú)立同分布的發(fā)射信號(hào)序列；C(k)是信道脈沖響應(yīng),；n(k)是高斯白噪聲序列,；y(k)是前饋濾波器輸出；z(k)是判決器的輸入,；w(k)表示判決器的輸出信號(hào),。

　　設(shè)前饋濾波器和反饋均衡器的輸入信號(hào)向量分別為：

　　x(k)=［x(k),x(k-1),…,x(k-Lf+1)］T（1）

　　w(k)=［w(k-1),w(k-2),…,w(k-Ld)］T（2）

　　前饋濾波器和反饋均衡器的權(quán)系數(shù)向量分別為：

　　F(k)=［f0(k),f1(k),…,fLf-1(k)］（3）

　　B(k)=［b0(k),b1(k),…,bLd-1(k)］T（4）

　　則由圖1可知：

　　z(k)=FT(k)x(k)-BT(k)w(k)（5）

　　式中，Lf和Ld分別為前饋濾波器長(zhǎng)度和反饋濾波器的長(zhǎng)度,，Lf,、Ld均為正整數(shù)，T表示轉(zhuǎn)置,。

　　則基于CMA的DFE盲均衡算法的權(quán)系數(shù)迭代公式為：

　　f(k+1)=f(k)-ufe(k)z(k)y*(k)

　　b(k+1)=b(k)+ube(k)z(k)w*(k)（6）

　　式（1）～式（6）構(gòu)成的算法稱為基于CMA的DFE盲均衡算法,。式(6)中，e(k)=|z(k)|2-R,，R為常數(shù)模算法的模值,，R=E［|s(k)|4］/E［|s(k)|2］，‘*’表示共軛,，uf和ub均為正實(shí)常數(shù),，分別為前饋濾波器和反饋濾波器更新方程中固定的迭代步長(zhǎng)。即基于CMA的DFE算法采用的是固定步長(zhǎng)的常數(shù)模算法來調(diào)整前饋濾波器和反饋濾波器的權(quán)系數(shù),。所以算法收斂慢,，收斂后穩(wěn)態(tài)誤差較大。

2改進(jìn)的基于CMA的DFE盲均衡算法

　　2.1算法原理

　　為了提高基于CMA的DFE盲均衡算法的收斂速度，改善其均衡性能,，研究人員提出了變步長(zhǎng)思想［57］,，即在保證收斂的情況下，在迭代初期為了加快收斂速度,，步長(zhǎng)取較大的值，在算法接近收斂時(shí),，為了減小穩(wěn)態(tài)誤差,，步長(zhǎng)取較小的值。根據(jù)這一原則,，文獻(xiàn)［5］提出了一種基于Sigmoid函數(shù)的變步長(zhǎng)盲均衡算法,，即構(gòu)造了一個(gè)關(guān)于瞬時(shí)誤差和步長(zhǎng)因子的單調(diào)Sigmoid函數(shù)，改進(jìn)算法不但具有較快的收斂速度且具有較小的穩(wěn)態(tài)誤差,。但Sigmoid函數(shù)過于復(fù)雜,，而且誤差在接近零處變化太大，不具有緩慢變化的特性,。對(duì)此本文對(duì)Sigmoid函數(shù)進(jìn)行了改進(jìn),，即通過引入均方誤差作為調(diào)整步長(zhǎng)的參量，構(gòu)造出指數(shù)型變步長(zhǎng)函數(shù),，具體表達(dá)式如下：

　　u(k)=c{1-exp［-d］}(7)

　　其中,，c，d為正常數(shù),，用于調(diào)整算法收斂速度及穩(wěn)態(tài)誤差,。

　　將式(7)代入式(6)，則抽頭系數(shù)權(quán)向量的更新方程變?yōu)?

　　f(k+1)=f(k)-u(k)e(k)z(k)y*(k)

　　b(k+1)=b(k)+u(k)e(k)z(k)w*(k)(8)

　　式（1）~（5）和式（8）構(gòu)成的算法稱為改進(jìn)的基于CMA的DFE盲均衡算法,。

　　2.2算法的收斂性分析

　　為了確保算法具有良好的收斂性和穩(wěn)健性,，步長(zhǎng)因子必須滿足：

　　0≤u(k)≤2/3tr(R)(9)

　　式（9）中，R代表輸入信號(hào)的自相關(guān)矩陣,，tr(R)代表該矩陣的跡,。

　　由式（7）可知：

　　0≤1-exp［-d］}≤1(10)

　　所以有：

　　0≤c{1-exp［-d］}≤c(11)

　　即：

　　0≤u(k)≤c(12)

　　所以c的取值要滿足：

　　c≤2/3tr(R)(13)

　　但滿足該條件的所有c和d對(duì)于步長(zhǎng)的取值大小存在著局限性，為此c和d的取值要由理論分析,、仿真分析和試驗(yàn)來共同確定,。

3仿真

　　為了驗(yàn)證新算法的性能，分別對(duì)基于CMA的DFE盲均衡算法和改進(jìn)的基于CMA的DFE盲均衡算法進(jìn)行了MATLAB仿真,。

　　仿真環(huán)境：發(fā)射信號(hào)采用4QAM的調(diào)制信號(hào),，信噪比為25 dB，前饋濾波器長(zhǎng)度為L(zhǎng)f=33,，采用中心抽頭初始化的方法,；反饋濾波器長(zhǎng)度Ld=17，抽頭系數(shù)初始化為全零值,；迭代次數(shù)N=4 000,，蒙特卡洛次數(shù)取400,。在兩種不同的信道中對(duì)兩種算法進(jìn)行仿真。

　　3.1實(shí)驗(yàn)1

　　信道為：h=［-0.053,0.184,-0.35,0,0,1］,，基于CMA的DFE算法中前饋和反饋濾波器的迭代步長(zhǎng)分別為0.000 75和0.06,，改進(jìn)的基于CMA的DFE算法中的步長(zhǎng)按式(8)調(diào)整，變步長(zhǎng)調(diào)整參數(shù)c,、d分別為0.007和6.0,，仿真結(jié)果如圖2所示。

　　圖2(a)表明改進(jìn)的基于CMA的DFE盲均衡算法大概經(jīng)過1 500次迭代收斂,，而基于CMA的DFE盲均衡算法大概需要經(jīng)過2 500次迭代之后才趨于收斂,，新算法比原算法將近快了1 000步。另外,，由圖2(a)可知,，改進(jìn)的基于CMA的DFE盲均衡算法的穩(wěn)態(tài)誤差比較小。圖2(b),、(c)表明,，與基于CMA的DFE盲均衡算法相比，改進(jìn)的基于CMA的DFE盲均衡算法輸出信號(hào)星座圖更加緊密集中,、清晰,，即改進(jìn)算法取得了更好的均衡效果。

　　3.2實(shí)驗(yàn)2

　　信道為：h=［0.212 2,0.104,0.890 8,0.213 4,-0.15,-0.083］,，基于CMA的DFE算法中前饋和反饋濾波器的迭代步長(zhǎng)分別為0.000 6和0.075,，改進(jìn)的基于CMA的DFE算法中的步長(zhǎng)按式(8)調(diào)整，變步長(zhǎng)調(diào)整參數(shù)c,、d分別為0.007和7.0,，仿真結(jié)果如圖3所示。

　　圖3(a)表明改進(jìn)的基于CMA的DFE盲均衡算法大概經(jīng)過2 000次迭代收斂,，而基于CMA的DFE盲均衡算法大概需要經(jīng)過3 000次迭代之后才趨于收斂,，新算法比原算法快了1 000步左右。另外,，由圖3(a)可知,，改進(jìn)的基于CMA的DFE盲均衡算法的穩(wěn)態(tài)誤差比較小。從圖3(b),、圖3(c)可以看出,，與基于CMA的DFE盲均衡算法相比，改進(jìn)的基于CMA的DFE盲均衡算法輸出信號(hào)星座圖更加緊密集中,、清晰,，即改進(jìn)算法取得了更好的均衡效果，具有更小的穩(wěn)態(tài)誤差。

4結(jié)束語

　　針對(duì)基于CMA的DFE盲均衡算法收斂速度慢,、收斂后穩(wěn)態(tài)剩余誤差大的缺點(diǎn),，構(gòu)造了一種改進(jìn)的基于CMA的DFE盲均衡算法。該算法把基于CMA的DFE盲均衡算法中前饋濾波器和反饋濾波器更新方程中的迭代步長(zhǎng)由原來的固定值改成可變值,，即通過引入均方誤差作為調(diào)整步長(zhǎng)的參量,，構(gòu)造出指數(shù)型變步長(zhǎng)函數(shù)。4QAM信號(hào)仿真結(jié)果表明,，相對(duì)于固定步長(zhǎng)的基于CMA的DFE盲均衡算法,，改進(jìn)算法不但具有較快的收斂速度而且具有較小的穩(wěn)態(tài)誤差。

　　參考文獻(xiàn)

　?。?］ 馮成旭，劉忠,，羅亞松.穩(wěn)健水聲信道判決反饋盲均衡算法研究［J］.火力與指揮控制,，2014,39(6):5-6.

　　［2］ 寧小玲,，劉忠,，羅亞松，等.一種改進(jìn)的水聲信道載波恢復(fù)盲均衡算法［J］.西安電子科技大學(xué)學(xué)報(bào),，2012,39(1):151-152.

　?。?］ 張銀兵，趙俊渭,，郭業(yè)才.抑制α穩(wěn)定噪聲的改進(jìn)常數(shù)模盲均衡算法［J］.西北工業(yè)大學(xué)學(xué)報(bào),，2010，28（2）:202-206.

　?。?］ 郭業(yè)才,，王南南.基于修正模判決的多模盲均衡算法研究［J］.計(jì)算機(jī)應(yīng)用研究，2014,31(8):2454-2455.

　?。?］ 劉建成,，趙宏志，全厚德,，等.迭代變步長(zhǎng)LMS算法及性能分析［J］.電子與信息學(xué)報(bào),，2015，37(7):1674-1675．

　?。?］ 宋志雄,，喻翌，趙海全.基于箕舌線函數(shù)的變步長(zhǎng)自適應(yīng)諧波電流檢測(cè)算法［J］.電力系統(tǒng)自動(dòng)化,，2013,37(22):54-59.

　?。?］ 張紅梅，韓萬剛.一種新的變步長(zhǎng)LMS自適應(yīng)濾波算法研究及其應(yīng)用［J］.儀器儀表學(xué)報(bào)，2015,36(8):1822-1830.