??? 摘 要： 在利用FPGA實現(xiàn)數(shù)字信號處理" title="數(shù)字信號處理">數(shù)字信號處理方面，分布式算法" title="分布式算法">分布式算法發(fā)揮著關鍵作用，與傳統(tǒng)的乘積-和結構相比,，具有并行處理的高效性特點。詳細研究了基于FPGA,、采用分布式算法實現(xiàn)FIR數(shù)字濾波器" title="數(shù)字濾波器">數(shù)字濾波器的原理和方法，并通過Xilinx ISE在Modelsim下進行了仿真,。
??? 關鍵詞： 分布式算法? DALUT? FPGA??? FIR
?
??? 數(shù)字濾波器正在迅速地代替?zhèn)鹘y(tǒng)的由R,、L、C元件和運算放大器組成的模擬濾波器并且日益成為DSP的一種主要處理環(huán)節(jié),。FPGA也在逐漸取代ASIC和PDSP,，用作前端數(shù)字信號處理的運算（如：FIR濾波、CORDIC算法或FFT）,。乘累加運算是實現(xiàn)大多數(shù)DSP算法的重要途徑,，而分布式算法則能夠大大提高乘累加運算的效能。
1 傳統(tǒng)的乘累加結構FIR數(shù)字濾波器基本理論
??? FIR濾波器被稱為有限長脈沖響應" title="脈沖響應">脈沖響應濾波器,，與IIR數(shù)字濾波器相對應,，它的單位脈沖響應h（n）只有有限個數(shù)據(jù)點。輸入信號經過線性時不變系統(tǒng)輸出的過程是一個輸入信號與單位脈沖響應進行線性卷積的過程,，即：
??? 
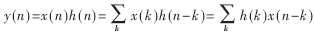
式中,，x(n)是輸入信號,，y(n)是卷積輸出，h(n)是系統(tǒng)的單位脈沖響應,?？梢钥闯觯看尾蓸觵(n)需要進行L次乘法和L-1次加法操作實現(xiàn)乘累加之和,，其中L是濾波器單位脈沖響應h(n)的長度,。可以發(fā)現(xiàn),，當L很大時,，每計算一個點，則需要很長的延遲時間,。
2 乘累加運算的位寬分配
??? DSP算法最主要的就是進行乘累加運算,。假設采樣信號的位寬用N來表示，則N位與N位的乘積結果需要2N位的寄存器來保存,；如果兩個操作數(shù)都是有符號數(shù)，則乘積只有2N-1個有效位,，因為產生了兩個符號位,。
??? 為了使累加器的結果不產生溢出，需要對累加器進行冗余設計,，也就是說要在累加器2N的位寬上多設計出K位,，累加器的長度M計算方式如下（L為濾波器的長度）：
??? 對于無符號數(shù)：M=2N+K=2N+log2L
????對于有符號數(shù)：M=2N+K=2N+log2L-1
3 乘累加運算的分布式算法原理分析
??? 得益于Xilinx FPGA查找表" title="查找表">查找表結構的潛能，分布式算法在濾波器設計方面顯示出了很高的效率,，自20世紀90年代初以來越來越受到人們的重視,。分布式算法是基于查找表的一種計算方法，在利用FPGA實現(xiàn)數(shù)字信號處理方面發(fā)揮著重要的作用,，可以大大提高信號的處理效率,。它主要應用于數(shù)字濾波、頻率轉換等數(shù)字信號處理的乘累加運算,。
??? 分布式算法推導如下：
??? 設Ak是已知常數(shù)（如濾波器系數(shù),、FFT中的正弦/余弦基本函數(shù)等），xk(n)是變量,，可以看作是n時刻的第k個采樣輸入數(shù)據(jù),，y(n)代表n時刻的系統(tǒng)響應。那么它們的內積為：
??? 
其中,，xk(n)變量可以寫成下面的格式：
??? 
式中,，B為數(shù)據(jù)格式的字長;xkb是變量的二進制位，只有“0”和“1”兩種狀態(tài),。將(2)式代入(1)式得：
??? 
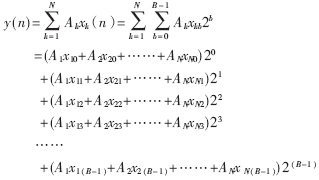
4 FPGA實現(xiàn)過程中查找表的構造方法
??? 根據(jù)以上論述,，括號中的每一乘積項代表著輸入變量的某一位與常量的二進制“與”操作,，加號代表著算術和操作，指數(shù)因子對括號中的值加權,。如果事先構造一個查找表,，該表存儲著括號中所有可能的組合值，就可以通過所有輸入變量相對應位的組合向量(xNb,x(N-1)b,…x1b)對該表進行尋址,，該查找表稱為DALUT,。DALUT的構造規(guī)則如表1所示。
?
??? 根據(jù)以上分析,，可以得出FPGA實現(xiàn)分布式算法的硬件結構,，如圖1所示。
?
5 采用分布式算法實現(xiàn)FIR數(shù)字濾波器
?? ?為了說明問題,，以一個三個系數(shù)的FIR數(shù)字濾波器為例設計分布式算法,，字寬也設置為三位。設FIR數(shù)字濾波器系數(shù)為：h(0)=5,h(1)=2,h(2)=3,。相對應的ADLUT表如表2所示,。
?
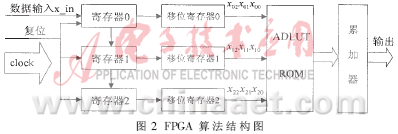
??? 在進行FPGA設計時，該表以組件Component形式構建,，設置為ROM結構,，提供輸入尋址端口table_in[2..0]，輸出端口table_out[3..0],。FPGA算法的結構圖如圖2所示,。
?
??? 算法實現(xiàn)中的幾個關鍵問題為：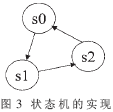
??? （1）采用狀態(tài)機實現(xiàn)分布式算法的狀態(tài)轉移
??? 狀態(tài)機的實現(xiàn)如圖3所示，設置三個狀態(tài)s0,、s1,、s2。狀態(tài)s0完成數(shù)據(jù)的裝入,，數(shù)據(jù)寄存器需要成對出現(xiàn),，一個完成數(shù)據(jù)的延遲，另一個完成數(shù)據(jù)的移位,，并將狀態(tài)轉移到s1,；狀態(tài)s1完成查找表功能、數(shù)據(jù)移位和分布式算法的乘累加運算,，數(shù)據(jù)移位一個數(shù)據(jù)寬度后將狀態(tài)轉移到s2,；狀態(tài)s2完成數(shù)據(jù)的輸出，并將狀態(tài)轉移到s0,。利用狀態(tài)機可以條理清楚地簡化計算過程,，在算法實現(xiàn)時發(fā)揮著關鍵的作用。
??? （2）系統(tǒng)時鐘與數(shù)據(jù)輸入時鐘的關系
??? 根據(jù)上述的狀態(tài)轉移關系，可以得出：每輸入一個數(shù)據(jù),，在下一次數(shù)據(jù)輸入之前,，需要在狀態(tài)s1停留一個數(shù)據(jù)寬度（三位）的時鐘時間，在s2停留一個時鐘的數(shù)據(jù)輸出時間,。也就是說,，系統(tǒng)時鐘頻率應是數(shù)據(jù)輸入頻率的5倍，即fclkock=5fxin,。
??? (3)分布式算法中的乘累加公式推導及核心代碼實現(xiàn)
?? ?設B是數(shù)據(jù)的字寬,，Pn是分布式算法第n位的結果，則有：
??? 
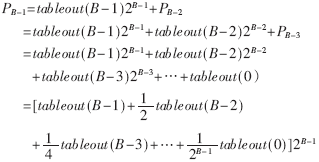
??? 有了該關系式,，就可以通過for...loop循環(huán),，使用一條語句完成分布式乘累加算法。具體如下：
??? for n in 0 to B-1 loop
???? ??P:=P/2+tableout(n)*2B-1;
??? end loop;
6 算法仿真驗證與結論
?? ?本文實現(xiàn)的FIR濾波器在Xilinx的集成開發(fā)環(huán)境ISE下利用ModelSim進行了仿真,。當輸入數(shù)據(jù)為7,3,1...時,，仿真輸出依次為35,29,32,16...，與乘累加方式FIR濾波算法得出的結果完全一致,。假設查找表和PDSP的通用乘法器延遲時間相同,，分布式算法的等待時間是B?子，通用乘法器的等待時間是NI,?？梢姡瑢τ谖粚捿^小的數(shù)據(jù)來說,，分布式算法的執(zhí)行速度遠高于乘累加運算?？梢?，利用FPGA實現(xiàn)分布式計算大大提高了計算的速度，在高速信號處理中發(fā)揮著重要作用,。
參考文獻
1劉 偉,，孟憲元.利用FPGA實現(xiàn)小型聲納的片上系統(tǒng)集成.電子技術應用，2000,；26（10）
2 盧 毅. VHDL與數(shù)字電路設計.北京：科學出版社, 2002
3 褚振勇. FPGA設計與應用. 西安:西安電子科技大學出版社,2002
4 程佩青.數(shù)字信號處理教程.北京：清華大學出版社,，2000