摘  要: 結(jié)合基于圖像塊的顯著性信息隨機(jī)采樣和基于投影Landweber的壓縮感知重構(gòu)算法,，提出了一種新的圖像壓縮感知編碼與重構(gòu)方法,。該方法在編碼端通過(guò)圖像顯著性信息來(lái)分配不同的測(cè)量維數(shù)以實(shí)現(xiàn)測(cè)量維數(shù)的自適應(yīng)，在重構(gòu)端,，通過(guò)在投影Landweber重構(gòu)算法中用不同的方向變換來(lái)得到重構(gòu)圖像,。與同類方法相比，在測(cè)量維數(shù)相同的前提下,，重構(gòu)圖像的峰值信噪比和主觀視覺(jué)效果都有很大的提高,。
關(guān)鍵詞: 壓縮感知； 顯著性信息,； 投影Landweber,； 方向變換

    壓縮感知CS(Compressed Sensing)[1]理論自從形成以來(lái)，便引起了學(xué)術(shù)界的廣泛關(guān)注,。壓縮感知是一種新興的信號(hào)采集,、編解碼理論，它突破了奈奎斯特采樣定理的瓶頸,。當(dāng)信號(hào)的采樣率小于信號(hào)帶寬的兩倍時(shí),，它依然能夠精確地重構(gòu)出原始信號(hào)，但前提條件是信號(hào)是可稀疏化的或是可壓縮的,。壓縮感知非常適合應(yīng)用于二維圖像,，但仍然面臨著許多棘手的問(wèn)題，例如測(cè)量矩陣的設(shè)定以及計(jì)算復(fù)雜度等。近幾年,，相繼提出了許多分塊[2]CS重構(gòu)的快速算法,，例如在投影Landweber迭代算法[3]中引入方向變換（CT[4]、DDWT[5]等）來(lái)完成快速CS重構(gòu),。然而,，這種方法在編碼端對(duì)圖像各個(gè)部分都采用了相同的測(cè)量維數(shù)，導(dǎo)致重構(gòu)圖像的質(zhì)量受到影響,。本文將基于顯著性信息[6]的壓縮感知編碼方法與加入了方向變換的投影Landweber重構(gòu)算法相結(jié)合,，提出了一種新的壓縮感知編碼與重構(gòu)方法，在編碼端根據(jù)圖像的顯著性信息來(lái)對(duì)各圖像塊分配不同的測(cè)量維數(shù),，從而實(shí)現(xiàn)測(cè)量維數(shù)的自適應(yīng),，以此來(lái)更好地保留圖像重要細(xì)節(jié)信息，達(dá)到增加重構(gòu)圖像質(zhì)量效果的目的,；而重構(gòu)時(shí)采用了參考文獻(xiàn)[3]中的方法,，在投影Landweber重構(gòu)算法中引入方向變換。大量實(shí)驗(yàn)結(jié)果表明,，與參考文獻(xiàn)[3]方法相比,，在測(cè)量維數(shù)相同的情況下，本文算法重構(gòu)的圖像質(zhì)量會(huì)有很大的提高,。

還是有可能的,。


2.2 方向變換
    現(xiàn)在圖像處理中廣泛地使用離散小波變換，但是傳統(tǒng)的離散小波變換是有缺陷的,，如平移不變性和顯著方向選擇性等,。因此，提出了比傳統(tǒng)的離散小波變換具有更高程度的方向表示的變換,，兩個(gè)最突出的變換就是Contourlet小波變換(CT)[4]和復(fù)數(shù)對(duì)偶樹(shù)小波變換(DDWT)[5]。CT小波變換保留了傳統(tǒng)離散小波變換的優(yōu)點(diǎn),，即多分辨率和信號(hào)的局部特征,，在犧牲了空間冗余的同時(shí)更好地代表圖像的方向特性。另外,，DDWT改進(jìn)了離散小波變換的不足之處,，它產(chǎn)生了一個(gè)比傳統(tǒng)的小波變換更具有方向性的分解，但是,，由于DDWT的兩個(gè)樹(shù)都是正交或是雙正交分解,，它總體來(lái)說(shuō)是一個(gè)冗余的緊密的框架。本文主要采用了DCT,、DWT,、CT和DDWT 4種變換。
3 基于顯著性信息和方向變換的圖像壓縮感知
    針對(duì)參考文獻(xiàn)[3]中所提方法在編碼端過(guò)于簡(jiǎn)單，本文將基于顯著性信息的壓縮感知算法與采用了方向變換的投影Landweber重構(gòu)算法有效地結(jié)合在一起,，充分利用基于顯著性信息的壓縮感知算法在編碼端自適應(yīng)分配測(cè)量維數(shù)的優(yōu)勢(shì)來(lái)對(duì)原方法進(jìn)行改進(jìn),，從而有效地提高了重構(gòu)圖像質(zhì)量。下面詳細(xì)介紹編碼端與重構(gòu)端的具體流程,。
3.1 編碼端
　在編碼端的實(shí)現(xiàn)步驟如下,。
    (1)對(duì)圖像進(jìn)行分塊[2]處理。為了方便測(cè)量矩陣的存儲(chǔ)和使用,，首先將原始圖像(nrow×ncol)分成若干個(gè)大小為B×B的塊來(lái)進(jìn)行處理(B=16),。
    (2)提取圖像塊的顯著性信息。根據(jù)1.2節(jié)的步驟來(lái)求出每個(gè)圖像塊的顯著性信息,，進(jìn)而求得整個(gè)圖像的顯著性信息,最終求得第i個(gè)圖像塊的顯著性信息所占的比值Ri,。
   

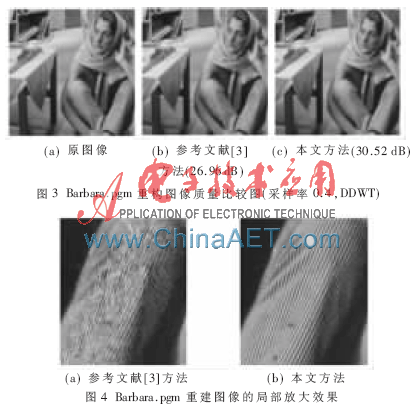
灰度圖像Lena.pgm和Barbara.pgm，圖像分塊大小為16×16,。表1是灰度圖像在采樣率分別為0.2,、0.3、0.4和0.5時(shí)兩種方法得到重構(gòu)圖像的PSNR性能比較結(jié)果,。實(shí)驗(yàn)結(jié)果表明,，本文所提出的方法能夠?qū)⒅貥?gòu)圖像的平均PSNR提高大約2 dB。圖3是采用灰度圖像Barbara.pgm,、方向變換為DDWT以及采樣率為0.4時(shí)得到的重構(gòu)圖像的主觀視覺(jué)效果比較,。圖4為Barbara.pgm重建圖像的局部放大結(jié)果比較。由所得重構(gòu)圖像的PSNR性能比較以及主觀視覺(jué)效果比較可以看出,，在相同的采樣率下,，本文方法能夠更好地保留圖像的重要細(xì)節(jié)信息且具有較少的重構(gòu)噪聲，因此具有視覺(jué)效果更好的重構(gòu)圖像,。

    本文通過(guò)分析基于投影Landweber的壓縮感知重構(gòu)算法,，針對(duì)其在編碼端過(guò)于簡(jiǎn)單的缺點(diǎn)，提出了一種基于顯著性信息和方向變換的圖像壓縮感知編碼與重構(gòu)方法,。該方法在編碼端實(shí)現(xiàn)了測(cè)量維數(shù)的自適應(yīng),，更好地保留了圖像的重要細(xì)節(jié)信息,提高了重構(gòu)圖像質(zhì)量。大量實(shí)驗(yàn)結(jié)果表明,，該方法與參考文獻(xiàn)[3]方法相比,，在具有相同測(cè)量維數(shù)的前提下，能夠很好地增加重構(gòu)圖像的峰值信噪比,，同時(shí)在重構(gòu)圖像的主觀視覺(jué)效果上也有很好的表現(xiàn),。
參考文獻(xiàn)
[1] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory,2006,52(4):1289-1306.
[2] GAN L. Block compressed sensing of natural images[C]. International Conference on Digital Signal Processing, 2007:403-406.
[3] MUN S, FOWLER J E. Block compressed sensing of images using directional transforms[C] .2009 International Conference on Image Processing,Cairo,2009:3021-3024.
[4] DO M N,VETTERLI M. The contourlet transform: an efficient directional multiresolution image representation[J]. IEEE Transactions on Image Processing,2005,14(12):2091-2106.
[5] SELESNICK I W, BARANIUK R G, KINGSBURY N G. The dual-tree complex wavelet transform[J]. IEEE Signal Processing Magazine,2005,22(6):123-151.
[6] Yu Ying, Wang Bin, Zhang Liming. Saliency-based compressive sampling for image signals[J]. IEEE Signal Processing Letters, 2010,17(11):973-976.
[7] PIANA M, BERTERO M. Projected landweber method and preconditioning[J]. Inverse Problems, 1997,13:441-464.
[8] HAUPT J, NOWAK R. Signal reconstruction from nosiy random projected[J].IEEE Transactions on Information Theory,2006,52(9):4036-4048.
[9] DONOHO D L. De-noising by soft-thresholding[J]. IEEE Transactions on Information Theory,1995,41(3):613-627.