0 引言

　　隨著無線通信技術(shù)的發(fā)展，寬帶數(shù)據(jù)業(yè)務(wù)量急增,，用戶對(duì)數(shù)據(jù)傳輸率和通信容量要求越來越高,，然而無線通信系統(tǒng)的頻譜和發(fā)射功率十分有限，如何充分利用有限的資源來滿足用戶成為當(dāng)前一個(gè)重要研究課題[1],。多輸入多輸出(Multiple Input Multiple Output,，MIMO)可以在不損傷頻帶和不增加發(fā)射功率條件下，成倍提高系統(tǒng)的通信容量,，較好地解決了頻帶資源緊缺難題,，因此多輸入多輸出技術(shù)成為當(dāng)前無線通信領(lǐng)域的研究熱點(diǎn)，受到人們?cè)絹碓蕉嗟年P(guān)注[2],。

　　在多輸入多輸出系統(tǒng)通信過程中,，由于受到多用戶、多天線造成的信道干擾,，嚴(yán)重影響了通信質(zhì)量,，成為多輸入多輸出系統(tǒng)應(yīng)用中的瓶頸問題[3]。為了解決該難題,，需要采用一定的技術(shù)對(duì)接收機(jī)和發(fā)射機(jī)兩端信號(hào)進(jìn)行處理,，預(yù)編碼技術(shù)在這種背景下應(yīng)運(yùn)而生[4],。預(yù)編碼的基本思想為：首先采集發(fā)射端的信道狀態(tài)信息，然后采用預(yù)編碼矩陣對(duì)信號(hào)進(jìn)行預(yù)處理,，消除用戶之間的干擾,，提高系統(tǒng)吞吐率，降低系統(tǒng)誤碼率,。預(yù)編碼算法分為兩類：線性和非線性預(yù)編碼,，其中線性預(yù)編碼算法主要有基于迫零（zero forcing，ZF）和最小均方誤差（minimum mean square error,，MMSE）兩種準(zhǔn)則[5,，6]，它們具有成本低,、復(fù)雜度低等優(yōu)點(diǎn),，在理想條件下可以降低用戶干擾,，但是通信性能比較差,；非線性的預(yù)編碼算法主要有模代數(shù)預(yù)編碼THP(Tomlinson-Harashima Precoding)等，THP算法融合了取模操作和串行干擾消除技術(shù),，可以更好地抑制噪聲,、誤碼率。然而,，當(dāng)信道狀態(tài)矩陣發(fā)生根本性變化,，THP算法的誤碼率急劇上升，為此有學(xué)者提出了基于格基約減算法(Lattice Reduction,，LR),，利用減格技術(shù)改良發(fā)射端信道狀態(tài)矩陣，可以有效抑制噪聲,，提高統(tǒng)性能[7],。LR算法是從一組給定的基出發(fā)，對(duì)其進(jìn)行不斷變換,，然后找到一組長(zhǎng)度更短的向量,，由于初始基不同，LR算法得到新基長(zhǎng)度也不同,，因此LR算法的效率和輸出基質(zhì)量與初始基選擇密切相關(guān)[8],。粒子群算法（Particle Swarm Optimization，PSO）是一種模擬鳥群覓食行為的群智能算法,，其將問題的可行解看作粒子群索,，然后每一個(gè)粒子根據(jù)自身和群全的飛行經(jīng)驗(yàn)在解的空間飛行，找到最優(yōu)解,，為L(zhǎng)R算法初始基的確定提供了一種新的研究思路[9],。

　　通過上面的分析,，為了提高多輸入多輸出系統(tǒng)的通信質(zhì)量，降低數(shù)據(jù)傳輸?shù)恼`碼率,，本文提出一種粒子群算法優(yōu)化LR的MIMO系統(tǒng)預(yù)編碼方案(PSO-LR),，最后通過仿真實(shí)驗(yàn)驗(yàn)證了其有效性和優(yōu)越性。

1 MIMO系統(tǒng)預(yù)編碼模型

　　多輸入多輸出通信系統(tǒng)的發(fā)送端和接收端包含多個(gè)天線,，其工作原理為：首先信號(hào)數(shù)據(jù)流通過發(fā)送端輸入到處理模塊中,，進(jìn)行編碼、調(diào)制和加權(quán),，然后將處理后的數(shù)據(jù)送到發(fā)射天線,，天線對(duì)信號(hào)進(jìn)行解調(diào)、匹配濾波,、譯碼等處理,，最后接收端輸出信號(hào)。設(shè)多輸入多輸出通信系統(tǒng)的接收端有K個(gè)移動(dòng)用戶,，每個(gè)移動(dòng)用戶擁有Nrk根天線,，預(yù)編碼技術(shù)是對(duì)多輸入多輸出通信系統(tǒng)發(fā)射端的信號(hào)進(jìn)行預(yù)處理，使發(fā)射信號(hào)更好的適應(yīng)信道狀況,，提升系統(tǒng)性能,，預(yù)編模型結(jié)構(gòu)具體如圖1所示[10]。

　　設(shè)wk表示用戶k的預(yù)編碼矩陣,，那么用戶k接收到的信號(hào)向量可以表示為：

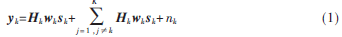
　　其中,，Hk表示用戶k的信道矩陣， sk表示發(fā)射信號(hào)的矢量,， nk表示高斯噪聲,。

　　式(1)可以簡(jiǎn)化為：

　　yk=Hk WS+ nk(2)

　　其中，W=[w1,，w2,，…，wK],，S=[s1,，s2，…,，SK]T,。

　　預(yù)編碼技術(shù)主要是消除多用戶之間干擾，預(yù)編碼矩陣可以采用如下公式計(jì)算得到,。

　　式中,， w是功率控制因子。

　　LR算法的核心是將H進(jìn)行分解，得到正交性更強(qiáng)的矩陣Hreal和一個(gè)幺模交換模矩陣U,，可以表示為：

　　H=Hreal U(4)

　　LR算法的關(guān)鍵點(diǎn)是找到最優(yōu)的矩陣Hreal,，其與H可構(gòu)成相同的格空間，因此本文將搜索能力強(qiáng)的粒子群算法引入到LR算法中找到得更優(yōu)的矩陣H,，以提高多輸入多輸出系統(tǒng)的通信質(zhì)量[11],。

2 MIMO系統(tǒng)預(yù)編碼方案

　　2.1 THP預(yù)編碼方案

　　THP預(yù)編碼是一種性能較優(yōu)的非線性預(yù)編碼方案，融合了算術(shù)取模和串行干擾消除技術(shù),，在判決反饋均衡器端進(jìn)行取模操作,，取輸入信號(hào)在星座圖上的邊界作為模，然后把均衡器的輸出映射到輸入端信號(hào)的星座圖上,，有效降低信號(hào)發(fā)射功率,，抑制傳輸過程中噪聲增強(qiáng)，其系統(tǒng)框架如圖2所示,，其中,，Mod表示取模操作，n表示加性噪聲,，B為對(duì)角線元素為1的上三角矩陣,，G是補(bǔ)償矩陣，主要用于消除取模操作的影響[12],。

　　由于當(dāng)信道狀態(tài)矩陣發(fā)生根本性變化,，THP預(yù)編碼算法的誤碼率將急劇上升,，為此有學(xué)者將LR算法與THP預(yù)編碼算法結(jié)合,，產(chǎn)生LR-THP預(yù)編碼算法。采用LR算法將信道狀態(tài)矩陣H轉(zhuǎn)換成為更好的新基,，然后據(jù)QR分解理論產(chǎn)生兩個(gè)矩陣,，這樣低級(jí)的子信道就會(huì)對(duì)高一級(jí)的子信道造成干擾。因此,，可以通過串行干擾消除技術(shù)消除子信道間干擾,，并采用THP取模操作將發(fā)射信號(hào)重新限制在輸入信號(hào)的范圍之內(nèi)。

　　LR算法只能在多項(xiàng)式時(shí)間內(nèi)找到一個(gè)長(zhǎng)度不超過格中最短向量長(zhǎng)度2(n-1)/2倍的向量,，為了獲得更優(yōu)的格基,，所以本文提出采用粒子群算法對(duì)LR算法的格基進(jìn)行優(yōu)化，以獲得更加理想的傳輸信息,。

　　2.2 LR算法

　　2004年,，LENSTRA A K等提出了一種性能優(yōu)異的格基約減算法(LR)，設(shè)存在一個(gè)矩陣B,，對(duì)B做QR分解得到B+QR,，如果三角矩陣R滿足下列條件：

　　則可稱B是格基約減的。

　　經(jīng)過LR算法約減之后能得到近似于最短向量的短向量,，而且經(jīng)過LR算法約減之后得到的新基的正交偏離度得到了極大的改善,，即正交性更強(qiáng)[13],。

　　2.3 粒子群算法

　　在標(biāo)準(zhǔn)粒子群算法中，每個(gè)粒子均具有自己的位置和速度,，n維解空間中每個(gè)粒子的位置代表優(yōu)化問題的一個(gè)可能解,。每個(gè)粒子根據(jù)自身的經(jīng)驗(yàn)和群體的經(jīng)驗(yàn)調(diào)整速度和位置，具體如下：

　　式中,，稱為慣性權(quán)重,，c1、c2為學(xué)習(xí)因子,，pbest表示粒子本身經(jīng)歷過的最好位置,，gbest表示種群經(jīng)歷過的歷史最好位置。

　　2.4 PSO-LR預(yù)編碼方案流程

　　初始格基的排列順序不同,，LR算法找到的新格基也不相同,，因此，可以通過置亂初始格基,，得到多組新的格基,，以這些格基作為候選解，然后采用粒子群算法找到最優(yōu)的格基,。

　　(1)粒子群的初始化,。對(duì)于格基約減算法而言，初始格基只有一個(gè),，即只有一個(gè)初始解,，只有通過對(duì)這一組格基進(jìn)行變換來生成其它的候選格基，構(gòu)成初始粒子群,，具體方式為,。

　　根據(jù)Bi=UiB就產(chǎn)生了m組基，便完成初始種群產(chǎn)生,。

　　(2)適應(yīng)度函數(shù)設(shè)計(jì),。適應(yīng)度值越差表示該個(gè)體的生存能力越弱，越易被淘汰,；反之表示該個(gè)體的生存能力很強(qiáng),。個(gè)體適應(yīng)能力優(yōu)劣通常采用適應(yīng)度函數(shù)進(jìn)行描述，因此,，在粒子飛行過程中,，適應(yīng)度函數(shù)指導(dǎo)種群進(jìn)化的方向，也是指引最優(yōu)解的搜索空間,。設(shè)基格L的其中一組約減基b,，其約減基首向量長(zhǎng)度為y1(b)，約減基的平均向量長(zhǎng)度為y2(b)，那么適應(yīng)度函數(shù)定義為：

　　式中,，w1,、w2表示權(quán)值，A表示種群的集合,。

　　本文的粒子群算法優(yōu)化LR算法的流程如圖3所示,，工作步驟如下：

　　步驟1：將一組格基b1，b2,，…,，bn進(jìn)行置亂，產(chǎn)生包含m個(gè)體的初始粒子群,。

　　步驟2：將每一個(gè)粒子的適應(yīng)度值與個(gè)體歷史最優(yōu)值進(jìn)行比較,，如果更優(yōu)，則用當(dāng)前粒子位置替換自身歷史最優(yōu)位置,。

　　步驟3：將每一個(gè)粒子的適應(yīng)度值與群體歷史最優(yōu)值進(jìn)行比較,，如果更優(yōu)，則用當(dāng)前粒子位置替換種群歷史最優(yōu)位置,。

　　步驟4：根據(jù)式(4)和式(6)更新粒子的速度,、位置。

　　步驟5：如果滿足算法終止要求,，則輸出適應(yīng)度最高的一組格基,，否則返回步驟2繼續(xù)進(jìn)行優(yōu)化。

3 仿真實(shí)驗(yàn)

　　3.1 仿真環(huán)境

　　為了測(cè)試本文預(yù)編碼算法的性能,，在AMD Athlon (tm) II X2 250 3.00 GHz CPU,、4G RAM的Windows XP系統(tǒng)平臺(tái)上，采用MATLAB 2009b進(jìn)行仿真實(shí)驗(yàn),，以測(cè)試算法在4×4多輸入多輸出系統(tǒng),，4QAM和16QAM調(diào)制方式下的性能。信道模型采用靜態(tài)瑞利平坦衰落信道,，每個(gè)用戶的發(fā)射功率相等，仿真次數(shù)為2 000,，在相同配置條件下,，與采用LR-THP、MMSE-THP算法進(jìn)行對(duì)比實(shí)驗(yàn),。

　　3.2 結(jié)果與分析

　　LR-THP,、MMSE-THP以及PSO-LR算法的仿真結(jié)果如圖4、圖5所示,。

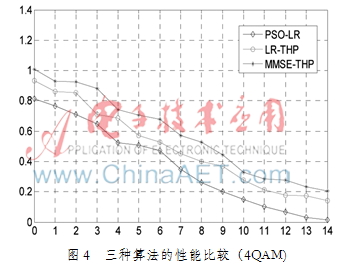
　　對(duì)圖4,、圖5進(jìn)行對(duì)比和分析，可以得到如下結(jié)論：

　　(1)當(dāng)信噪比較小時(shí)，LR-THP,、MMSE-THP以及PSO-LR算法的性能相差不大,，隨著信噪比增加，3種算法的誤碼率(BER)不斷下降,，相對(duì)于MMSE-THP算法,，LR-THP、PSO-LR算法的性能具有明顯的優(yōu)勢(shì),，這主要是由于LR-THP,、PSO-LR算法采用了基于格基約減的THP預(yù)編碼方案，通信質(zhì)量得以明顯改善,，對(duì)比結(jié)果驗(yàn)證了采用基于格基約減預(yù)編碼方案的有效性和優(yōu)越性,。

　　(2)相對(duì)于LR-THP算法，PSO-LR算法的誤碼率更低,，這主要是因?yàn)椴捎昧Ｗ尤核惴▽?duì)初始格基進(jìn)行優(yōu)化和選擇,，可以得到長(zhǎng)度更短的向量和質(zhì)量更高的一組新基，從而提高了格基約減算法的運(yùn)行效率,，一定程度保證了傳輸數(shù)據(jù)的可靠性,。

4 結(jié)束語

　　本文針對(duì)當(dāng)前格基約減算法存在的不足，充分利用粒子群算法的優(yōu)點(diǎn),，提出了一種基于粒子群算法優(yōu)化格基約減的預(yù)編碼機(jī)制,，并通過仿真實(shí)驗(yàn)測(cè)試算法的性能。仿真結(jié)果表明相對(duì)于傳統(tǒng)預(yù)編碼方案,，在相同條件下,，PSO-LR預(yù)編碼機(jī)制有效降低了誤碼率，提高了通信質(zhì)量,。然而在現(xiàn)代移動(dòng)通信中,，不僅要考慮通信質(zhì)量，同時(shí)還考慮算法的復(fù)雜度,，因此如何更好的平衡性能和復(fù)雜度之間的關(guān)系是我們將來研究的重點(diǎn),。

　　參考文獻(xiàn)

　　[1] 范文兵，趙龍賀,，王綠靜.單環(huán)模型下三維多極化天線MIMO信道建模[J].電視技術(shù),，2013，37(23)：179-182.

　　[2] 周圍,，吳敏子.基于分組的ML-SIC的MIMO聯(lián)合檢測(cè)算法[J].電視技術(shù),，2013，37(15)：16-128.

　　[3] GAN Y H,，LING C.Complex lattice reduction algorithm for low-complexity full diversity MIMO detection[C].IEEE Transactions on signal processing,，2009,，57(7)：2701-2710.

　　[4] WESEL R D，CIOFFI J M.Precoding and the MMSE-DFE.Signals[J].Systems and Computers,，2013(2)：1144-1148.

　　[5] MA G D,，WU M Q，XU C X,，et al.Lattice-reduction-aided Tomlinson-Harashima precoding based on MMSE criteria in multi-user MIMO downlink system[J].Communi-cation Technology and Application,，2011，12：98-102.

　　[6] WINDPASSINGER C,，F(xiàn)ISCHER R,，HUBER J B.Lattice-reduction-aided broadcast precoding[J].Communications[J].IEEE Transactions，2004,，52(12)：2057-2060.

　　[7] DAMEN M O,，CAIRE G.On Maximum likelihood detection and the Search for the closest Lattice Point[J].IEEE Trans-actions on information theory，2003,，49(10)：2389-2402.

　　[8] 劉向輝,，韓文報(bào)，權(quán)建校.基于遺傳策略的格基約化算法[J].電子與信息學(xué)報(bào),，2013,，35(8)：1940-1945.

　　[9] 方旺盛，曾苑,，岳崇倫.基于粒子群優(yōu)化和小波變換的視頻水印算法[J].電視技術(shù),，2013，37(1)：122-125.

　　[10] 張慶榮,，王剛.LR算法在MIMO_LAS_CDMA系統(tǒng)中的應(yīng)用[J].吉林大學(xué)學(xué)報(bào)：信息科學(xué)版,，2006(1)：12-17.

　　[11] 趙曉群，章惜珍,，屈非,，等.MIMO系統(tǒng)LLL格基約減檢測(cè)技術(shù)研究[J].大連民族學(xué)院學(xué)報(bào)，2011,，13(1)：19-23.

　　[12] ARBERO Lg,，RATNARAJAH T，COWAN C.A comparison of complex lattice reduction algorithms for MIMO detection[J].IEEE International conferences on Acoustics,，2008,，4(1)：2705-2708.

　　[13] ZHANG W，QIAO S Z,，WEI Y M.HKZ and Minkowski reduction algorithms for lattice-reduction-aided MIMO detection[J].Signal Processing，IEEE,，2012,，60(11)：5963-5976.