0 引言

　　自適應(yīng)濾波器可廣泛應(yīng)用于系統(tǒng)識別、信號處理和數(shù)字通信等許多領(lǐng)域,。而超大規(guī)模集成電路和FPGA的飛速發(fā)展,，也促進了自適應(yīng)濾波技術(shù)的進步。此外,，由于其對干擾頻率不敏感,，且其權(quán)值調(diào)整是基于對系統(tǒng)參數(shù)的優(yōu)化，因此,，自適應(yīng)濾波器仍然越來越多地受到人們的關(guān)注,。

　　1 LMS自適應(yīng)濾波器

　　1．1 LMS算法

　　最小均方誤差(LMS)算法具有計算量小、易于實現(xiàn)等優(yōu)點,，因此,，在實踐中被廣泛應(yīng)用。LMS算法的基本思想是調(diào)整濾波器自身的參數(shù),，使濾波器的輸出信號與期望輸出信號之間的均方誤差最小,，并使系統(tǒng)輸出為有用信號的最佳估計,。實質(zhì)上，LMS可以看成是一種隨機梯度或者隨機逼近算法,，可以寫成如下的基本迭代方程：

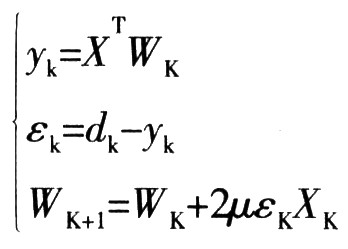
　　其中,，μ為步長因子，是控制穩(wěn)定性和收斂速度的參量,。從上式可以看出,，該算法結(jié)構(gòu)簡單、計算量小且穩(wěn)定性好,，但固定步長的LMS算法在收斂速度,、跟蹤速率及權(quán)失調(diào)噪聲之間的要求相互制約。為了克服這一缺點,，人們提出了各種變步長的LMS改進算法,，主要是采用減小均方誤差或者以某種規(guī)則基于時變步長因子來跟蹤信號的時變，其中有歸一化LMS算法(NLMS),、梯度自適應(yīng)步長算法,、自動增益控制自適應(yīng)算法、符號一誤差LMS算法,、符號一數(shù)據(jù)LMS算法,、數(shù)據(jù)復(fù)用LMS算法等。

　　1．2 LMS自適應(yīng)濾波器的結(jié)構(gòu)原理

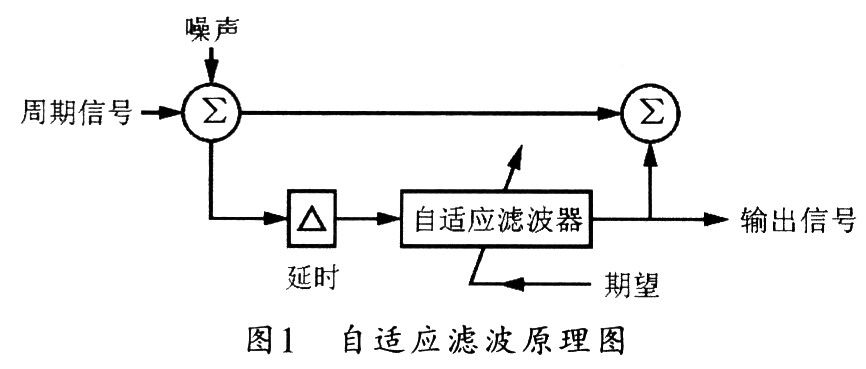
　　自適應(yīng)濾波是在部分信號特征未知的條件下,，根據(jù)某種最佳準則,，從已知的部分信號特征所決定的初始條件出發(fā)，按某種自適應(yīng)算法進行遞推,，在完成一定次數(shù)的遞推之后,，以統(tǒng)計逼近的方式收斂于最佳解。當(dāng)輸入信號的統(tǒng)計特性未知,，或者輸入信號的統(tǒng)計特性變化時,。自適應(yīng)濾波器能夠自動地迭代調(diào)節(jié)自身的濾波器參數(shù)．以滿足某種準則的要求，從而實現(xiàn)最優(yōu)濾波,。因此,，自適應(yīng)濾波器具有自我調(diào)節(jié)和跟蹤能力。在非平穩(wěn)環(huán)境中,，自適應(yīng)濾波在一定程度上也可以跟蹤信號的變化,。圖1 為自適應(yīng)濾波的原理框圖。

　　2 LMS濾波器的仿真與實現(xiàn)

　　2．1 LMS算法參數(shù)分析

　　傳統(tǒng)的LMS算法是最先由統(tǒng)計分析法導(dǎo)出的一種實用算法．它是自適應(yīng)濾波器的基礎(chǔ),。通過Matlab仿真對LMS算法中各參數(shù)的研究,，總結(jié)出其對算法的影響。現(xiàn)針對時域LMS算法的各參數(shù)進行一些討論,。

　　(1)步長

　　步長μ是表征迭代快慢的物理量,。由LMS算法可知：該量越大,，自適應(yīng)時間μ越小，自適應(yīng)過程越快,，但它引起的失調(diào)也越大,，當(dāng)其大于1／λmax時，系統(tǒng)發(fā)散,；而該值越小,，系統(tǒng)越穩(wěn)定，失調(diào)越小,，但自適應(yīng)過程也相應(yīng)加長,。因此，對步長μ的選擇應(yīng)從整個系統(tǒng)要求出發(fā),，在滿足精度要求的前提下,，盡量減少自適應(yīng)時間,。

　　(2)級數(shù)

　　自適應(yīng)濾波器的級數(shù)應(yīng)與噪聲通道的傳遞函數(shù)F(z)的階數(shù)一致,。事實上，只有在二者相等時,，自適應(yīng)濾波器傳遞函數(shù)才有可能等于F(z),，以實現(xiàn)噪聲抵消。而當(dāng)其級數(shù)小于F (z)的階數(shù)時,，參考通道的噪聲將無法與輸入通道的噪聲抵消,，故會引起最小均方差增大；當(dāng)其級數(shù)大于F(z)的階數(shù)時,，過多的級數(shù)則會引起失調(diào)的增大,。因此，只有當(dāng)濾波器的級數(shù)等于F(z)的階數(shù)時,，自適應(yīng)濾波器的性能才能達到最佳,。

　　(3)信噪比

　　當(dāng)信噪比升高時，LMS算法的性能將急劇惡化,。故可采用頻域LMS算法來克服時域LMS算法的性能局限,。

　　2．2 DSP Builder建模

　　采用Altera公司的FPGA器件可進行數(shù)字信號的處理設(shè)計。Altera公司提供有可視化的開發(fā)工具軟件DSP Builder,。利用它可在MATIAB的圖形仿真環(huán)境Simulink中建立一個*mdl模型文件,，同時在DSP Builder和其他Simulink庫中找到相應(yīng)的圖形模塊并調(diào)入Simulink窗口。圖2所示為4階LMS濾波器模型界面,。利用其強大的圖形化仿真和分析功能,，可以分析系統(tǒng)的正確性。

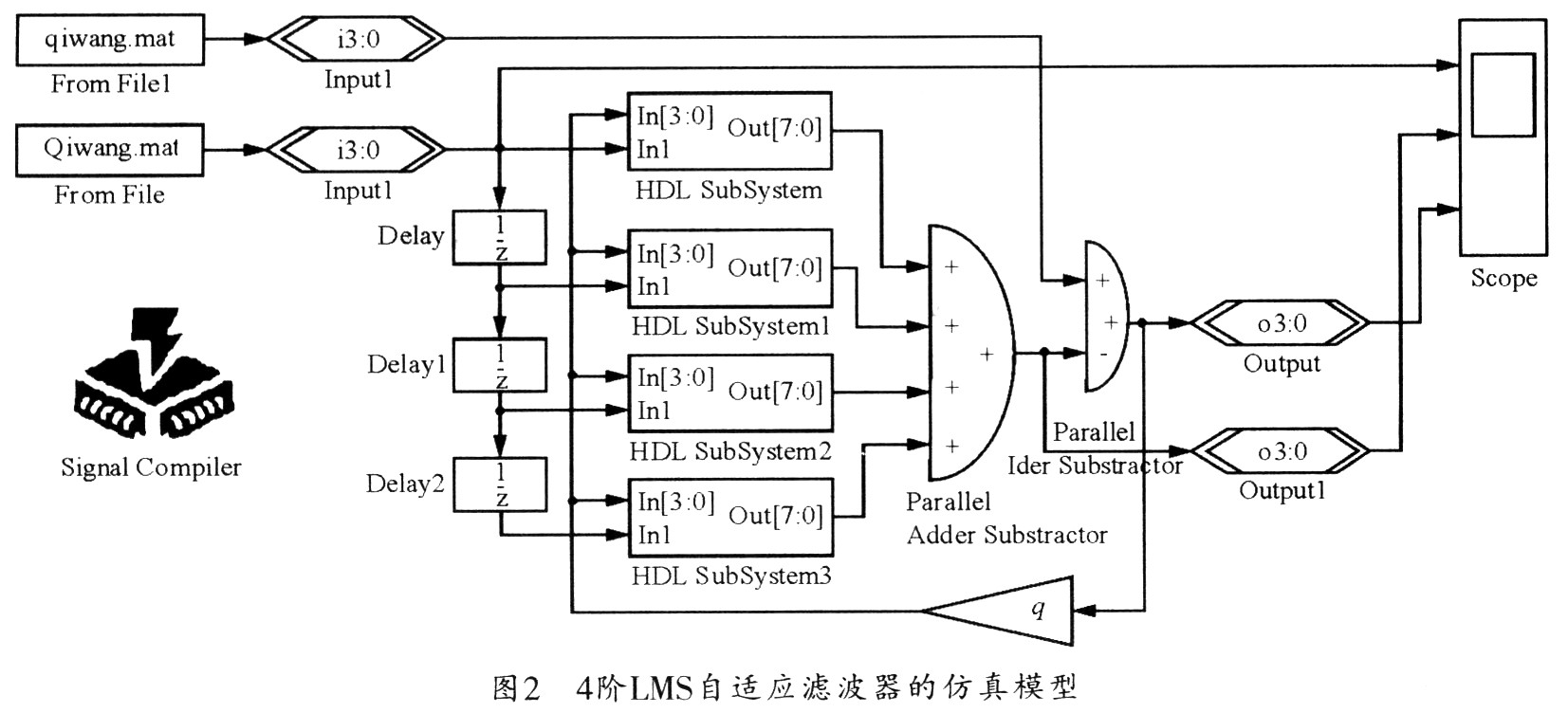
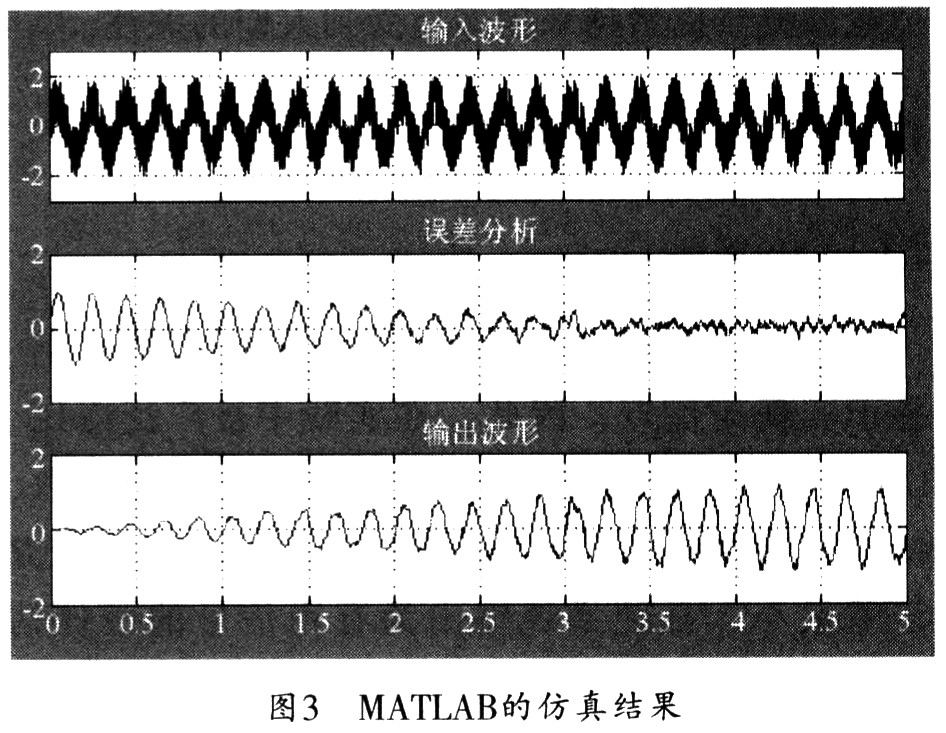
 　　圖中以shuru．mat為輸入信源,，qiwang．mat為期望,，信宿為Scope,。除圖中這些模塊外，還有一些總線控制模塊和權(quán)系數(shù)控制模塊,。其運行模型觀察的顯示結(jié)果如圖3所示,。在這種FIR濾波器的LMS算法中，其誤差將隨著權(quán)的逼近逐漸減小,，但沒有等于零,，而是在零值上下起伏，這說明了LMS算法是用平方誤差代替均方誤差而造成的誤差缺點,。

　　3 基于FPGA的實現(xiàn)方法

　　模型通過以后,，運行SigalCompiler可將模型轉(zhuǎn)化成VHDL語言和Tcl腳本。由于在Simuilnk中進行的模型仿真是算法級的,，屬于系統(tǒng)驗證性質(zhì)的仿真,，并沒有對VHDL代碼進行仿真。而生成的VHDL代碼是RTL級且是針對具體的硬件結(jié)構(gòu)的,，因此,，轉(zhuǎn)化后的VHDL代碼實現(xiàn)就可能與*mdl模型描述的情況不符，故有必要再對生成的RTL級VHDL代碼進行功能驗證,。ALTERA公司的ModelSim平臺是使用最廣泛的基于單內(nèi)核的VerilogHDL/VHDL混合仿真器,，利用它可方便地將信號波形顯示為類似模擬信號的格式，特別適合顯示復(fù)雜信號的波形,。這給仿真調(diào)試帶來了極大的方便,。在QuartusⅡ調(diào)用上述文件，便可用ModelSim對生成的VHDL代碼進行功能級仿真,。轉(zhuǎn)化成功后再調(diào)用VHDL綜合器進行綜合并生成底層網(wǎng)表文件,。然后再調(diào)用OuartusⅡ進行編譯，接著用QuartusⅡ根據(jù)網(wǎng)表文件及設(shè)置的優(yōu)化約束條件進行布線布局和優(yōu)化設(shè)計的適配,，最后生成編程文件和仿真文件,。這樣，生成的POF／SOF FPGA配置文件便可用于對目標(biāo)器件的編程配置和硬件實現(xiàn),。

　　4 結(jié)束語

　　本文采用自上而下的設(shè)計思想,，并用FPGA實現(xiàn)了自適應(yīng)濾波器。同時用MATIAB和OuartersⅡ混合仿真實現(xiàn)了LMS算法的設(shè)計方案,。結(jié)果表明,，該自適應(yīng)濾波器具有良好的消燥能力。