摘 要： 給出了神經(jīng)網(wǎng)絡魯棒性的概念，基于系統(tǒng)辨識的BP網(wǎng)絡,、RBF網(wǎng)絡和Elman網(wǎng)絡的魯棒性問題進行了分析和研究,。仿真結果表明，神經(jīng)網(wǎng)絡用于非線性系統(tǒng)辨識有其廣闊的前景,。
關鍵詞： 魯棒性 神經(jīng)網(wǎng)絡 系統(tǒng)辨識
?
在控制系統(tǒng)的研究中,，人們關心的最基本的問題是系統(tǒng)的穩(wěn)定性在參數(shù)變化下保持的可能性。Davison在提出干擾不變性的內模原理時提出了系統(tǒng)結構穩(wěn)定性的概念,，這是一種基于無窮小擾動分析的魯棒性概念,。在實際系統(tǒng)中參數(shù)既不能視為不變，也不能僅具有無窮小擾動,。系統(tǒng)工作環(huán)境的變化,，模型的不精確性、降階近似,、非線性的線性化等都可化成一種參數(shù)擾動,。有時系統(tǒng)受控對象可能有幾個不同的工作狀態(tài)。當用同一控制器來控制時,，人們也把不同工作狀態(tài)所對應的參數(shù)差別視為一種擾動,，這種參數(shù)的變化只能被視為有界擾動。現(xiàn)代魯棒性分析的最重要的特點就是要求討論在有界擾動下系統(tǒng)性能保持的能力,。
常系數(shù)線性系統(tǒng)魯棒分析與氯控制正取得豐富的成果,，但非線性系統(tǒng)的魯棒性研究還是十分必要的。神經(jīng)網(wǎng)絡的非線性系統(tǒng)變換為非線性系統(tǒng)尤其是工業(yè)過程系統(tǒng)的辨識與控制提供了有效的途徑,。本文針對三種用于工業(yè)過程控制的典型神經(jīng)網(wǎng)絡(BP,、Elman、RBF網(wǎng)絡)算法的魯棒性,，進行了分析,、比較和研究，最后給出了仿真結果。
1 三種神經(jīng)網(wǎng)絡的魯棒性分析
有的文獻將神經(jīng)網(wǎng)絡的魯棒性與泛化能力混為一談,，比如將采用雙BP算法,，使網(wǎng)絡輸入值變化很小時，網(wǎng)絡輸出值基本不變看成是網(wǎng)絡的泛化性,。所以首先要明確什么是神經(jīng)網(wǎng)絡的魯棒性,。對于前向無反饋神經(jīng)網(wǎng)絡而言，神經(jīng)網(wǎng)絡的魯棒性是指當輸入信息或神經(jīng)網(wǎng)絡發(fā)生有限攝動時,，神經(jīng)網(wǎng)絡仍能保持正常的輸入—輸出關系的特性,；對于反饋神經(jīng)網(wǎng)絡而言，神經(jīng)網(wǎng)絡的魯棒性是指當輸入信息或神經(jīng)網(wǎng)絡發(fā)生有限攝動時,，神經(jīng)網(wǎng)絡仍能保持穩(wěn)定的輸入—輸出關系的特性,。
神經(jīng)網(wǎng)絡的魯棒性依賴于神經(jīng)網(wǎng)絡參數(shù)位置和它附近系統(tǒng)誤差曲面的具體形態(tài)。神經(jīng)網(wǎng)絡參數(shù)設計在極值點附近而其附近的形態(tài)誤差曲面又比較平緩時,，網(wǎng)絡的魯棒性就好,，否則魯棒性就差。使系統(tǒng)誤差曲面在設計處平緩的主要方法是選用平滑的變換函數(shù),，但平滑的變換函數(shù)又不利于提高網(wǎng)絡的學習速度,。BP網(wǎng)絡、Elman網(wǎng)絡,、RBF網(wǎng)絡的變換函數(shù)都是平滑的,，所以問題的關鍵就是網(wǎng)絡參數(shù)能否在極值點附近。
下面通過一個動態(tài)系統(tǒng)的實例進行分析,。
動態(tài)系統(tǒng)的函數(shù)映射關系式為：
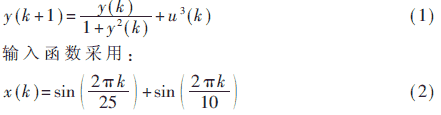
圖1給出了系統(tǒng)的輸入—輸出延遲—輸出的三維圖,，把輸入和輸出延遲都作為自變量時，就為利用靜態(tài)網(wǎng)絡辨識靜態(tài)系統(tǒng)提供了可能性,。
該動態(tài)系統(tǒng)的函數(shù)映射關系實際是基于NARMA模型的函數(shù)形式,，因此可以把系統(tǒng)輸入、輸出和它們的延遲值同時作為靜態(tài)神經(jīng)網(wǎng)絡的輸入,，從而使得靜態(tài)神經(jīng)網(wǎng)絡能映射NARMA模型類的動態(tài)系統(tǒng),。NARMA模型是一種統(tǒng)一的有限可實現(xiàn)非線性系統(tǒng)的表達式。
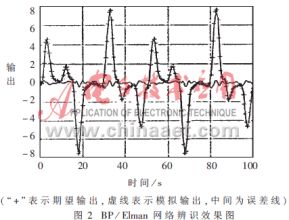
圖2,、圖3分別為BP/Elman,、RBF網(wǎng)絡辨識系統(tǒng)的效果圖。
2 仿真結果
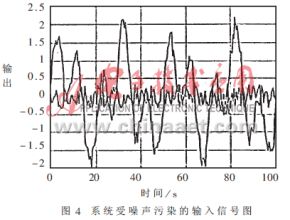
在上述所研究的系統(tǒng)中的輸入上附加一隨機量,，如圖4所示,。它類似于工業(yè)過程中的噪聲污染。
?
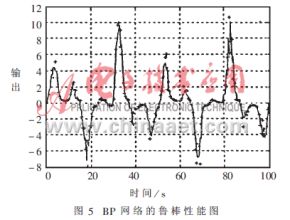
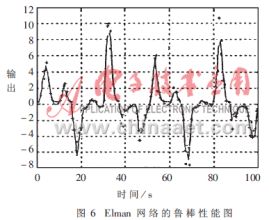
通過訓練好的神經(jīng)網(wǎng)絡來模擬輸出,，并與系統(tǒng)的實際輸出比較,。從圖5,、圖6、圖7中可明顯看出BP網(wǎng)絡,、Elman網(wǎng)絡的模擬輸出比較光滑,，沒有出現(xiàn)大的躍變，且與實際輸出差值不大,，而RBF網(wǎng)絡與前者的最大差別是會出現(xiàn)大幅度的躍變,。這是由于噪聲的影響，受噪聲污染的輸入偏離了訓練樣本集中的輸入,，從而偏離了徑向基函數(shù)的中心，這樣其輸出與真實值相差就很大,。
?
從仿真結果中可知：RBF網(wǎng)絡的最大優(yōu)點是收斂速度快,、逼近精度高、訓練結果唯一,；而最大的不足是泛化性能較差,，所以當其輸入偏離訓練樣本集時，系統(tǒng)表現(xiàn)出的魯棒性就會很差,。但它在時變快,、學習樣本集可基本覆蓋整個系統(tǒng)的狀態(tài)的情況下具有明顯的優(yōu)越性。所以針對系統(tǒng)的辨識與控制研究神經(jīng)網(wǎng)絡的魯棒性是非常必要的,。
參考文獻
1 黃 琳,，王 龍，于年才.系統(tǒng)魯棒性的若干問題——背景,、現(xiàn)狀與挑戰(zhàn).控制理論及應用,，1991;8(1)：11～12
2 張邦禮，李銀國,，曹長修.非線性系統(tǒng)神經(jīng)網(wǎng)絡辨識的魯棒BP算法.控制與決策,，1996;11(1)：26～27