文獻(xiàn)標(biāo)識(shí)碼: A
DOI:10.16157/j.issn.0258-7998.2015.12.016
中文引用格式: 何川,李智,王勇軍. 基于STM32的四旋翼飛行器的姿態(tài)最優(yōu)估計(jì)研究[J].電子技術(shù)應(yīng)用,2015,41(12):61-64.
英文引用格式: He Chuan,Li Zhi,Wang Yongjun. Research on attitude optimal estimation of quad-rotor aircraft based on STM32[J].Application of Electronic Technique,2015,41(12):61-64.
0 引言
姿態(tài)最優(yōu)估算是飛行器自主飛行的先決條件,在飛行過(guò)程中,實(shí)時(shí)準(zhǔn)確地獲得飛行器的姿態(tài)信息,可以決定飛行器的控制精度和穩(wěn)定性[1]。隨著微電子技術(shù)的發(fā)展,飛行器姿態(tài)解算系統(tǒng)普遍采用低成本的航姿參考系統(tǒng)(AHRS),其主要包括:基于微機(jī)電系統(tǒng)(MEMS)的三軸陀螺儀、三軸加速度計(jì)和三軸磁羅盤(pán)。由于系統(tǒng)機(jī)械結(jié)構(gòu)和傳感器自身三軸并非完全正交,引入了不正交誤差,以及數(shù)據(jù)積分產(chǎn)生的發(fā)散誤差和外部干擾產(chǎn)生的隨機(jī)誤差。因此要估計(jì)飛行器姿態(tài)的最優(yōu)信息必須對(duì)多傳感器進(jìn)行誤差處理,并尋求最佳數(shù)據(jù)融合算法。
目前國(guó)內(nèi)對(duì)MEMS傳感器姿態(tài)解算系統(tǒng)研究的常用算法有:擴(kuò)展卡爾曼濾波、梯度下降法、互補(bǔ)濾波等。擴(kuò)展卡爾曼濾波應(yīng)用非常廣泛,但為其建立可靠穩(wěn)定的狀態(tài)方程、確定合適的量測(cè)噪聲和過(guò)程噪聲協(xié)方差矩陣都比較困難。梯度下降法的好處在于姿態(tài)解算過(guò)程只有普通的乘法和加法運(yùn)算,普通的微控制器即能滿足算法要求,但難點(diǎn)在于構(gòu)造合適的目標(biāo)函數(shù)[2]。本系統(tǒng)在Mahony[3]提出的補(bǔ)償濾波器的基礎(chǔ)上進(jìn)行優(yōu)化,采用雙環(huán)補(bǔ)償濾波算法,外環(huán)引用重力場(chǎng)和地磁場(chǎng)進(jìn)行補(bǔ)償,內(nèi)環(huán)引用重力場(chǎng)進(jìn)行補(bǔ)償,并將修正后的陀螺儀和磁羅盤(pán)進(jìn)行互補(bǔ)濾波,以期得到最優(yōu)姿態(tài)輸出。
1 飛行器姿態(tài)描述
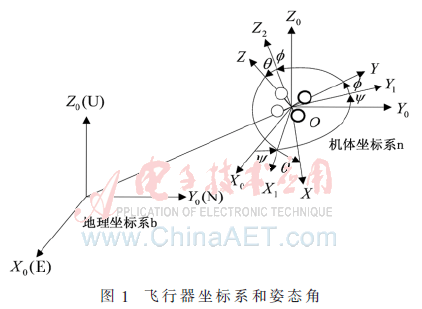
飛行器常用的姿態(tài)描述方法有歐拉角、方向余弦矩陣和四元數(shù)三種。三維空間中,飛行器有3個(gè)轉(zhuǎn)動(dòng)自由度,分別可以通過(guò)3個(gè)角度參數(shù)來(lái)描述飛行器的姿態(tài),分別定義為:繞機(jī)體坐標(biāo)系的Z軸轉(zhuǎn)動(dòng)為偏航角Ψ;繞X軸轉(zhuǎn)動(dòng)為橫滾角φ;繞Y軸轉(zhuǎn)動(dòng)為俯仰角θ[4]。

由于載體的運(yùn)動(dòng),四元數(shù)Q=[q0 q1 q2 q3]T是變量,q0、q1、q2、q3是時(shí)間函數(shù)。剛體繞瞬時(shí)轉(zhuǎn)軸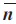 轉(zhuǎn)過(guò)σ角度來(lái)實(shí)現(xiàn)坐標(biāo)的轉(zhuǎn)換。
轉(zhuǎn)過(guò)σ角度來(lái)實(shí)現(xiàn)坐標(biāo)的轉(zhuǎn)換。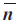 為參考坐標(biāo)系下的一個(gè)單位矢量,其角速度為:
為參考坐標(biāo)系下的一個(gè)單位矢量,其角速度為:

機(jī)體坐標(biāo)系n和地理坐標(biāo)系b之間的變換也可以用四元數(shù)的三角形式表示[6]:

在忽略地球的自轉(zhuǎn)和公轉(zhuǎn)運(yùn)動(dòng)對(duì)四旋翼飛行器造成的影響,并假設(shè)飛行器為剛體運(yùn)動(dòng)且質(zhì)量分布對(duì)稱、均勻,中心為重心位置且不隨著運(yùn)動(dòng)而發(fā)生變化[7],則四元數(shù)矩陣表達(dá)式Q的微分方程解為:


2 飛行器姿態(tài)解算系統(tǒng)構(gòu)建
2.1 系統(tǒng)硬件
本姿態(tài)解算系統(tǒng)硬件主要包括主控制器和航姿參考系統(tǒng)(AHRS)。其中主控器采用ST(意法半導(dǎo)體)公司的Cortex-M4為內(nèi)核的32位ARM微控制器STM32F405RGT6;航姿參考系統(tǒng)采用2款高精度的姿態(tài)傳感器,分別為:InvenSense公司的MPU-6500和ST公司的LSM303D,構(gòu)成了一個(gè)九軸的姿態(tài)測(cè)量系統(tǒng)。傳感器均選用數(shù)字芯片,內(nèi)部均集成有高精度的ADC。主控制器通過(guò)SPI總線,讀取出傳感器采集到的原始數(shù)據(jù),然后通過(guò)四元數(shù)的坐標(biāo)換算、姿態(tài)誤差的雙環(huán)PI控制和互補(bǔ)濾波解算出歐拉角。姿態(tài)解算系統(tǒng)框圖如圖2所示。
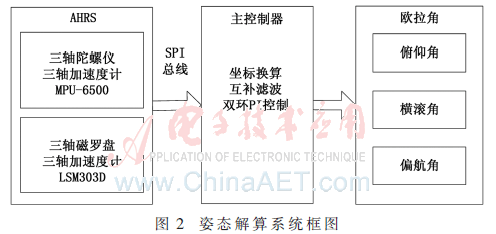
2.2 傳感器數(shù)據(jù)標(biāo)定
在數(shù)據(jù)融合之前需要對(duì)傳感器測(cè)量得到的原始數(shù)據(jù)進(jìn)行標(biāo)定,從而消除傳感器的零點(diǎn)偏置誤差。陀螺儀消除偏置誤差的方法是保持器件水平位置不變,多次采集后求取輸出平均值;加速度計(jì)消除偏置方法為八面校準(zhǔn)法,將飛行器姿態(tài)解算系統(tǒng)保持機(jī)頭方向不變,正面朝上、下、左、右、前、后和機(jī)頭朝上、機(jī)頭朝下。在這八種狀態(tài)下分別測(cè)量三軸加速度計(jì)ADC輸出的X、Y、Z三軸的最大最小值,并與±1 g(重力加速度)所對(duì)應(yīng)的ADC數(shù)值進(jìn)行校準(zhǔn);磁羅盤(pán)零點(diǎn)數(shù)據(jù)誤差采用橢圓假設(shè)法進(jìn)行標(biāo)定,將姿態(tài)解算系統(tǒng)分別在坐標(biāo)系下XOY和XOZ兩個(gè)平面內(nèi)360°旋轉(zhuǎn),并將采集到的數(shù)據(jù)用MATLAB軟件擬合成橢圓,然后修正橢圓的偏心和半徑。
3 系統(tǒng)數(shù)據(jù)融合與姿態(tài)解算
系統(tǒng)姿態(tài)解算分為兩個(gè)部分。第一部分是雙環(huán)PI控制器修正數(shù)據(jù)融合后傳感器偏差。第二部分為修正后的三軸陀螺儀與三軸磁羅盤(pán)進(jìn)行互補(bǔ)濾波,消除磁羅盤(pán)的高頻干擾,提高磁羅盤(pán)的響應(yīng)能力和抗干擾能力。姿態(tài)解算流程圖如圖3所示。
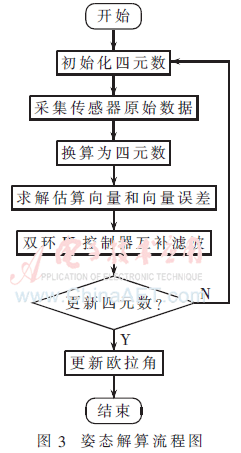
3.1 雙環(huán)PI控制器
陀螺儀可以快速響應(yīng)機(jī)體的旋轉(zhuǎn),短時(shí)間誤差較小、可信度高,但是存在溫漂和零漂,以及積分誤差隨時(shí)間累積等因素影響。加速度計(jì)在靜止的狀態(tài)下漂移很小,傾角求解過(guò)程不存在積分誤差,但是受到飛行過(guò)程中電機(jī)和機(jī)架的振動(dòng)以及轉(zhuǎn)動(dòng)和運(yùn)動(dòng)加速度的干擾。磁羅盤(pán)測(cè)量得到的地磁向量在一定地理范圍內(nèi)可以認(rèn)為不會(huì)發(fā)生改變,但是,磁羅盤(pán)容易受到硬磁場(chǎng)和軟磁場(chǎng)的干擾。
因此,系統(tǒng)外環(huán)采用九軸姿態(tài)傳感器(三軸加速度計(jì)、三軸磁羅盤(pán)和三軸陀螺儀)數(shù)據(jù)融合。由于磁羅盤(pán)容易受到干擾,有可能導(dǎo)致外環(huán)九軸數(shù)據(jù)融合后依舊存在較大誤差,所以,內(nèi)環(huán)采用六軸姿態(tài)傳感器(三軸加速度計(jì)和三軸陀螺儀)數(shù)據(jù)融合,對(duì)數(shù)據(jù)融合后的傳感器姿態(tài)偏差進(jìn)行二次修正。
外環(huán)九軸姿態(tài)傳感器數(shù)據(jù)融合,記在飛行器機(jī)體坐標(biāo)系下an=[ax ay az]T和mn=[mx my mz]T分別為加速度計(jì)和磁羅盤(pán)實(shí)際測(cè)量得到的重力向量和地磁向量。記vn=[vx vy vz]T和wn=[wx wy wz]T是將地理坐標(biāo)系下重力向量kb=[0 0 1g]T和地磁向量nb=[nx 0 nz]T(不考慮地理磁偏角因素,將機(jī)頭固定向北)通過(guò)四元數(shù)坐標(biāo)換算成機(jī)體坐標(biāo)系下的重力向量和地磁向量。向量之間的誤差為坐標(biāo)軸的旋轉(zhuǎn)誤差,可以用向量的叉積en=[ex ey ez]T表示,如式(6)所示。由于陀螺儀是對(duì)機(jī)體直接積分,所以,陀螺儀的誤差可以體現(xiàn)為機(jī)體坐標(biāo)的誤差。因此修正坐標(biāo)軸的誤差可以達(dá)到修正陀螺儀誤差的目的,從而將加速度計(jì)和磁羅盤(pán)進(jìn)行修正陀螺儀,實(shí)現(xiàn)了九軸的數(shù)據(jù)融合。即如果陀螺儀按照叉積誤差的軸,轉(zhuǎn)動(dòng)叉積誤差的角度,就可以消除機(jī)體坐標(biāo)上實(shí)際測(cè)量的重力向量和地磁向量和坐標(biāo)換算后的重力向量和地磁向量之間的誤差。
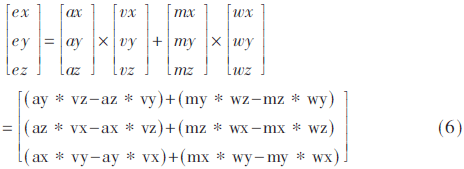
PI調(diào)節(jié)器的比例部分用于迅速糾正陀螺儀誤差,積分部分用于消除穩(wěn)態(tài)偏差[7]。通過(guò)大量實(shí)驗(yàn)驗(yàn)證后取PI調(diào)節(jié)器的比例系數(shù)為1.0,積分系數(shù)為0.2。陀螺儀經(jīng)過(guò)外環(huán)PI控制器修正姿態(tài)誤差后輸出值為gn=[gx gy gz]T:

3.2 互補(bǔ)濾波
本系統(tǒng)姿態(tài)解算的第二部分是磁羅盤(pán)的修正,主要采用互補(bǔ)濾波算法。互補(bǔ)濾波算法簡(jiǎn)單可靠且對(duì)器件精度要求低。互補(bǔ)濾波的目的在于將陀螺儀和磁羅盤(pán)各自在頻域角度上進(jìn)行互補(bǔ)。因?yàn)榇帕_盤(pán)動(dòng)態(tài)響應(yīng)能力差且易受外界環(huán)境的干擾,而陀螺儀動(dòng)態(tài)響應(yīng)快,故可在頻域上將二者形成互補(bǔ),即對(duì)磁羅盤(pán)低通濾波,對(duì)陀螺儀進(jìn)行高通濾波。如圖4所示,將修正后得到的陀螺儀數(shù)據(jù)與磁羅盤(pán)數(shù)據(jù)進(jìn)行互補(bǔ)濾波,即可消除磁羅盤(pán)的高頻干擾。
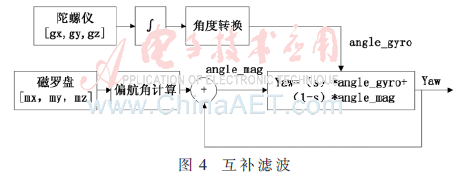

如式(10)所示,r為互補(bǔ)濾波中的權(quán)值,r值越大,證明陀螺儀占的權(quán)重越大。
4 姿態(tài)解算結(jié)果分析
為了驗(yàn)證姿態(tài)解算系統(tǒng)在多旋翼飛行器實(shí)際飛行過(guò)程中的性能,搭建了一個(gè)半實(shí)物仿真平臺(tái)。將基于STM32的姿態(tài)解算系統(tǒng)的四旋翼飛行器機(jī)頭朝向地理正北方,機(jī)架底部水平固定在萬(wàn)向節(jié)一端,萬(wàn)向節(jié)另外一端固定在水平的桌面上。啟動(dòng)四旋翼飛行器電機(jī),將飛行器油門通道值保持在空中懸停狀態(tài),及四個(gè)螺旋槳產(chǎn)生的向上的合力等于飛行器自身重力。然后,通過(guò)串口讀取出傳感器采集到的原始數(shù)據(jù)以及姿態(tài)解算后的數(shù)據(jù),并用MATLAB進(jìn)行數(shù)據(jù)分析。
圖5中采集的是模擬定點(diǎn)懸停時(shí)俯仰角和橫滾角。由于單純地通過(guò)陀螺儀采集得到的角速度進(jìn)行積分得到角度會(huì)產(chǎn)生積分誤差,并且積分誤差會(huì)隨著時(shí)間進(jìn)行累加,所以未進(jìn)行姿態(tài)解算所得到的姿態(tài)角零點(diǎn)誤差會(huì)不斷變大。圖中的2條線分別代表姿態(tài)解算后的橫滾角和俯仰角。由于采用了雙環(huán)PI修正陀螺儀,所以姿態(tài)角零點(diǎn)誤差與解算前相比不會(huì)隨著時(shí)間累計(jì)不斷變大。但是由于姿態(tài)解算系統(tǒng)處于四旋翼飛行器模擬定點(diǎn)懸停狀態(tài),所以,電機(jī)引起的機(jī)架振動(dòng)、載體重力分布不均、機(jī)械連接處阻尼問(wèn)題等因素,導(dǎo)致零點(diǎn)誤差相對(duì)于水平放置在桌面上時(shí)的靜態(tài)零點(diǎn)誤差,偏差較大且波動(dòng)相對(duì)厲害。零點(diǎn)誤差基本穩(wěn)定在±2.2°以內(nèi)。隨著時(shí)間的推移,零點(diǎn)誤差逐步趨近平穩(wěn),可以滿足四旋翼飛行器對(duì)姿態(tài)數(shù)據(jù)的要求。
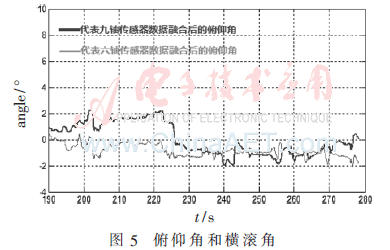
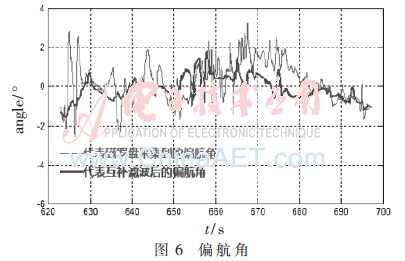
圖6中測(cè)試結(jié)果分別代表磁羅盤(pán)姿態(tài)解算前采集的數(shù)據(jù)和姿態(tài)解算后測(cè)量的數(shù)據(jù)。本系統(tǒng)采用的互補(bǔ)濾波算法中權(quán)值r取0.15,偏航角以磁羅盤(pán)采集的數(shù)據(jù)為主,數(shù)據(jù)融合后的陀螺儀只進(jìn)行輔助修正。可以觀測(cè)到細(xì)線代表的是沒(méi)有使用濾波算法的磁羅盤(pán)測(cè)量的偏航角,零點(diǎn)誤差相對(duì)較大,達(dá)到了±3°左右,而且上下波動(dòng)也很大,表示磁羅盤(pán)受到外界環(huán)境嚴(yán)重干擾。粗線代表磁羅盤(pán)和陀螺儀經(jīng)過(guò)互補(bǔ)濾波后采集得到的偏航角,消除了部分干擾信號(hào),上下波動(dòng)明顯減弱,并且誤差穩(wěn)定保持在±1.7°以內(nèi)。由于磁羅盤(pán)自身具有不可忽略的零位、靈敏度及非正交誤差,因此通過(guò)軟件算法無(wú)法徹底消除零點(diǎn)誤差。
5 結(jié)論
旋翼飛行器飛行過(guò)程中獲得姿態(tài)最優(yōu)估計(jì)是飛行器系統(tǒng)穩(wěn)定運(yùn)行的根本保障。本文基于四元數(shù)坐標(biāo)換算,將地理坐標(biāo)系下的重力向量和地磁向量換算到機(jī)體坐標(biāo)系下。然后通過(guò)修正坐標(biāo)系旋轉(zhuǎn)誤差,實(shí)現(xiàn)了多傳感器的數(shù)據(jù)融合,避免了陀螺儀零點(diǎn)積分誤差的累積,并將修正后的陀螺儀與磁羅盤(pán)進(jìn)行互補(bǔ)濾波,消除了磁羅盤(pán)的高頻干擾。實(shí)驗(yàn)表明:經(jīng)過(guò)雙環(huán)PI控制修正姿態(tài)偏差的陀螺儀,俯仰角和橫滾角零點(diǎn)動(dòng)態(tài)誤差保持在±2.2°左右;互補(bǔ)濾波后的磁羅盤(pán)消除了部分高頻干擾,偏航角誤差保持在±1.7°左右。本文設(shè)計(jì)的姿態(tài)解算系統(tǒng)較好地解決了噪聲干擾與姿態(tài)最優(yōu)估計(jì)問(wèn)題,并在半實(shí)物仿真平臺(tái)上得到了驗(yàn)證,實(shí)現(xiàn)了長(zhǎng)時(shí)間穩(wěn)定地輸出準(zhǔn)確可靠的姿態(tài)數(shù)據(jù),滿足了四旋翼飛行器飛行控制對(duì)姿態(tài)信息的要求。
參考文獻(xiàn)
[1] 張浩,任芊.四旋翼飛行器航姿測(cè)量系統(tǒng)的數(shù)據(jù)融合方法[J].兵工自動(dòng)化,2013,32(1):28-31.
[2] 杜杉杉,吳昊,張繼文,等.一種面向AHRS的改進(jìn)互補(bǔ)濾波融合算法[J].國(guó)外電子測(cè)量技術(shù),2015(3):13-18.
[3] MAHONY R,HAMEL T.Complementary filters on the special orthogonal group[C].IEEE Transactions on Automatic Control,2008,53(5):1203-1218.
[4] 張?zhí)旃猓跣闫迹觖愊?捷聯(lián)慣性導(dǎo)航技術(shù)[M].北京:國(guó)防工業(yè)出版社,2007:15-16.
[5] 鄧正隆.慣性技術(shù)[M].哈爾濱:哈爾濱工業(yè)大學(xué)出版社,2006:10-11.
[6] 李一波,宋述錫.基于模糊自整定PID四旋翼無(wú)人機(jī)懸停控制[J].控制工程,2013(5):910-914.
[7] 廖懿華,張鐵民,廖貽泳.基于模糊-比例積分偏差修正的多旋翼飛行器姿態(tài)測(cè)算系統(tǒng)[J].農(nóng)業(yè)工程學(xué)報(bào),2014(20):19-27.

